第 3回目の主題 :
![]()
いよいよ収束性の定義を述べよう。
がなりたつときに言う。
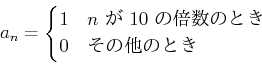
で定義するとき、
(証明) 背理法で、![]() がある数
がある数 ![]() に収束したとする。
収束の定義の
に収束したとする。
収束の定義の ![]() として
として
![]() を採用しよう。
ある
を採用しよう。
ある ![]() が存在して、
が存在して、
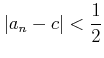 |
(※) |
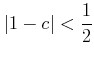
がわかり、
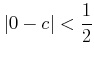
がわかる。
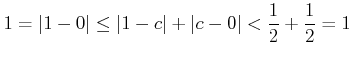
となって矛盾である。
よって、![]() はいかなる値にも収束しない。
はいかなる値にも収束しない。
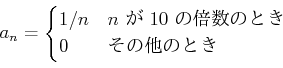
で定義するとき、
(証明)
与えられた
![]()
![]()
![]() にたいして、
にたいして、
![]() として、
として、
![]() より大きい整数を一つとっておく。
(そのようなもの(すなわち与えられた実数よりも大きな整数)
が存在することは、「アルキメデスの原理」として
保証されているが、マアさしあたっては当り前だと思っても良い。)
より大きい整数を一つとっておく。
(そのようなもの(すなわち与えられた実数よりも大きな整数)
が存在することは、「アルキメデスの原理」として
保証されているが、マアさしあたっては当り前だと思っても良い。)
この ![]() が収束の定義の
が収束の定義の ![]() の役割を果たすことを示そう。
実際、
の役割を果たすことを示そう。
実際、 ![]() なる任意の
なる任意の ![]() にたいして、
にたいして、
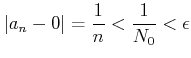
となって、いずれの場合にせよ
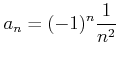
で定義するとき、
念のためアルキメデスの原理のステートメントを述べておこう。
を満たすものが存在する。
全体を ![]() で割っておけば、次のように言い換えてもよい:
どのような実数に対しても、それよりも大きな正の整数が
存在する。
で割っておけば、次のように言い換えてもよい:
どのような実数に対しても、それよりも大きな正の整数が
存在する。