![]()
今回から、関数の話に話題の重点をうつす。
これから、
「![]() の近くで定義されている(実数値)関数
の近くで定義されている(実数値)関数 ![]() 」
という言い方をもちいることがある。これは、
次の二つの状況が同時に満足されていることを
言い表す言葉である。
」
という言い方をもちいることがある。これは、
次の二つの状況が同時に満足されていることを
言い表す言葉である。
![]() は実数
は実数 ![]() の近くで定義された関数であるとする。このとき、
の近くで定義された関数であるとする。このとき、
![]() が
が ![]() に近づくときの
に近づくときの ![]() の極限値 は
の極限値 は ![]() である
(「
である
(「![]() のとき
のとき ![]() は
は ![]() に収束する」とも言う)
とは、
に収束する」とも言う)
とは、
が満たされるときに言う。
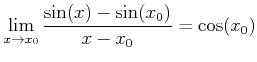
のような不定形の極限を相手にすることが多いからである。 )
とかく。