


Next: About this document ...
微分積分学概論AI要約 No.12

定義 12.1 (``§3 (I)(p.18)'')
実数のある区間
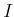
で定義された関数
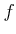
が狭義単調増加関数であるとは、
をみたすときにいう。
たまにこの条件を
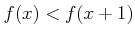 と同じと勘違いしている学生を
見かけるが、これはもちろん違う。
と同じと勘違いしている学生を
見かけるが、これはもちろん違う。
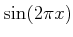 や、
や、
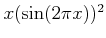 を考えてみれば良い。(ウラ面の図も参照)
を考えてみれば良い。(ウラ面の図も参照)
定理 12.2 (``定理17の系'')
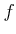
が閉区間
![$ [a,b]$](img8.png)
上の狭義単調増加な連続関数であれば、
の逆関数
が存在する。
さらに、この
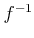
は連続で、かつ狭義単調増加である。
例 12.3
正の整数
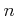
に対して、
0
以上の実数を定義域とする関数
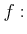
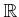
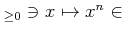
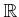
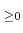
は連続であり、狭義単調増加である。この関数は全射でもあるから、
は逆写像を持つ。この関数を
と書く。
つまり
![% latex2html id marker 1015
$ y=\sqrt[n]{x}$](img18.png)
は
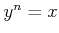
を満たす唯一の正の実数である。
命題 12.4
任意の正の実数
に対して、
がなりたつ。
Proof.
![% latex2html id marker 1031
$ y=\sqrt[n]{x}$](img23.png)
とおくと、定義により、
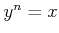
.
ゆえに、
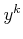
は
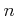
乗して
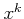
になる実数である。
そのような実数は唯一つ、すなわち
![% latex2html id marker 1043
$ \sqrt[n]{x^k}$](img27.png)
しかないのであるから、
両者は等しい。
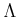
同様にして、次のことが分かる。
命題 12.5
正の整数
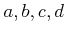
が
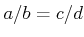
を満たせば、任意の実数
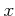
にたいして、
がなりたつ。
この命題がなりたつので、
![% latex2html id marker 1058
$ \sqrt[b]{x^a}$](img31.png) のことを
のことを
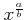 と
書いても誤解の恐れがない。
と
書いても誤解の恐れがない。
例 12.6
この例では、高校で習う三角関数の知識は
既知であるとする。
-
![$ [-\frac{\pi}{2},\frac{\pi}{2}] \ni x\mapsto \sin(x) \in [-1,1]$](img33.png) は狭義単調増加連続関数である。その逆関数のことを
は狭義単調増加連続関数である。その逆関数のことを
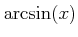 と書く。
と書く。
-
![$ [0,\pi] \ni x\mapsto \cos(x) \in [-1,1]$](img35.png) は狭義単調減少連続関数である。その逆関数のことを
は狭義単調減少連続関数である。その逆関数のことを
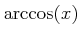 と書く。
と書く。
-
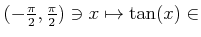
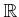 は狭義単調増加連続関数である。その逆関数のことを
は狭義単調増加連続関数である。その逆関数のことを
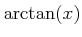 と書く。
と書く。
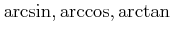 はそれぞれ
はそれぞれ
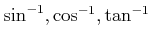 などと書くこともある。
などと書くこともある。
中間値の定理の証明が途中になってしまったので、ここでその証明を書いておこう。
![$ f: [a,b]\to$](img44.png)
 に対して、
に対して、
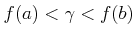 と仮定する。
と仮定する。
![$\displaystyle S=\{c \in [a,b]; \forall x \in [a,c]$](img46.png)
にたいして
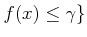
とおく。
仮定
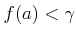 により
により 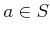 がわかる。
とくに、
がわかる。
とくに、
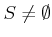 である。
他方で
である。
他方で 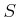 は
は ![$ [a,b]$](img8.png) の部分集合だから、
有界。ゆえに、
の部分集合だから、
有界。ゆえに、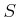 は上限
は上限 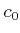 をもつ。
をもつ。
-
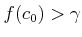 の場合。
の場合。
仮定 (
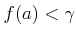 ) により
) により
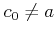 がわかる。
がわかる。
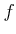 は
は 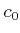 において連続であるから、
において連続であるから、
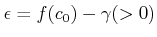 に対して、
ある
に対して、
ある 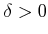 が存在して、
が存在して、
![$\displaystyle (x\in [a,b ]$](img57.png)
and
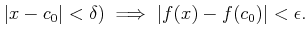
とくに、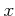 として
として
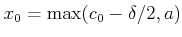 をとれば,
をとれば,
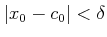 かつ
かつ
![$ x_0\in [a,b]$](img61.png) であるから、
であるから、
|
(12.1) |
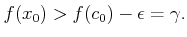 |
他方で 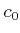 は
は  の上限であるから、
の上限であるから、
![$ S \cap (x_0,c_0]$](img63.png) には
ある元
には
ある元  が存在する。
が存在する。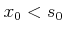 であることと、
であることと、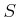 の定義を
みると、
の定義を
みると、
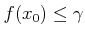 がわかる。 これは (12.1)式と矛盾する。
がわかる。 これは (12.1)式と矛盾する。
-
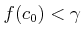 の場合。
の場合。
仮定 (
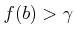 ) により
) により 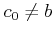 がわかる。
がわかる。
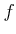 は
は 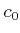 において連続であるから、
において連続であるから、
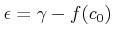 に対して、
ある
に対して、
ある 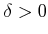 が存在して、
が存在して、
![$\displaystyle (x\in [a,b ]$](img57.png)
and
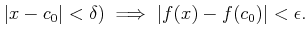
とくに、
![$ x\in (c_0-\delta, c_0+\delta)\cap [a,b]$](img71.png) なる
任意の
なる
任意の 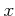 に対して、
に対して、
|
(12.2) |
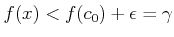 |
他方で 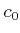 は
は  の上限であるから、
の上限であるから、
![$ S \cap (c_0-\delta,c_0]$](img73.png) には
ある元
には
ある元  が存在する。
が存在する。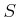 の定義により、
の定義により、
![$\displaystyle \forall x \in [a,s_0]$](img74.png)
に対して
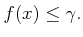
このことと (12.2)式を併せると、
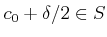 が結論され、
これは
が結論され、
これは 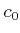 の定義に矛盾する。
の定義に矛盾する。
以上により、
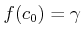 .
.
参考までに定義 12.1 の下の注意で述べた
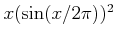 のグラフを
載せておこう。
のグラフを
載せておこう。
![\includegraphics[scale=0.5]{12-01.eps}](img79.png)



Next: About this document ...
2011-07-01
![]()
![]() と同じと勘違いしている学生を
見かけるが、これはもちろん違う。
と同じと勘違いしている学生を
見かけるが、これはもちろん違う。
![]() や、
や、
![]() を考えてみれば良い。(ウラ面の図も参照)
を考えてみれば良い。(ウラ面の図も参照)
![]()
![]() に対して、
に対して、
![]() と仮定する。
と仮定する。
![]() ) により
) により
![]() がわかる。
がわかる。
![]() は
は ![]() において連続であるから、
において連続であるから、
![]() に対して、
ある
に対して、
ある ![]() が存在して、
が存在して、
![]() ) により
) により ![]() がわかる。
がわかる。
![]() は
は ![]() において連続であるから、
において連続であるから、
![]() に対して、
ある
に対して、
ある ![]() が存在して、
が存在して、
![]() .
.
![]() のグラフを
載せておこう。
のグラフを
載せておこう。
![\includegraphics[scale=0.5]{12-01.eps}](img79.png)