![]()
は
![]()
![]() の定義を思い出しておこう。
の定義を思い出しておこう。
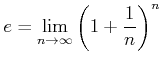
逆関数の定理により、![]() は
は ![]() の単調増加連続関数であることが
わかる。
の単調増加連続関数であることが
わかる。
数学では断らない限り対数の底としては ![]() をとり、
自然対数を考えるのが普通である。
をとり、
自然対数を考えるのが普通である。
上の定理は ![]() の
の ![]() の挙動を記述するものだが、
の挙動を記述するものだが、
![]() のときの挙動も大事である。
のときの挙動も大事である。
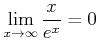
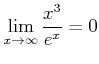
を証明せよ。
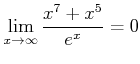
を証明せよ。
前回、
![]()
![]() が連続ならば
が連続ならば
![]()
![]() や
や
![]()
![]() も連続であることを証明(復習)した。
も連続であることを証明(復習)した。
このことは、つぎのようなことを使えば合成関数の連続性により 証明できてスッキリする。
問題12.1 解答。
任意の
![]() に対して、
に対して、
![]() とおく。
(
とおく。
( ![]() の代わりに
の代わりに
![]() を考えることによって、
を考えることによって、
![]() が大きい時の心配をしなくて済む。)
が大きい時の心配をしなくて済む。)
![]() とおく。
とおく。
![]() は
は
![]() となるような整数である。
そうしておいて、
となるような整数である。
そうしておいて、

![]() を
を
![]() を満たすような任意の有理数としよう。
すなわち、
を満たすような任意の有理数としよう。
すなわち、
No.12 の講義中に述べたように、
他方で、
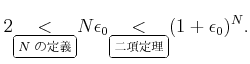
(二項定理のところは数学的帰納法の議論で置き換えても良い。) ゆえに、
(14.1), (14.2), (14.3) を組み合わせることにより、
すなわち、
がわかる。 ![]() ARRAY(0x8edbfa0)
ARRAY(0x8edbfa0)