- 持ち込みは何でも可である。ただし、他人の迷惑になるもの、 および通信機能をもつものを除く。
- 解答用紙には必ず学生番号と名前を記入すること。
- 解答用紙の裏面を用いてもよいが、その場合にはそれが分かるように 明記すること。
- この試験の解答例については http://www.math.kochi-u.ac.jp/docky/kogi/ からたどって見ることができるようにする予定である。
- 成績は理学部2号棟6F数学コース掲示板において確認できるようにする。 掲示があるまでは成績の照会等には応じられない。
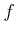 は 任意の
は 任意の
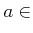
 において連続であることを定義に従って示しなさい。
において連続であることを定義に従って示しなさい。
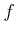 は
は ![$ [-5,5]$](img7.png) において一様連続であることを定義に従って示しなさい。
において一様連続であることを定義に従って示しなさい。
解答
(1)
任意の正の数
![]() に対して、
に対して、
![]() とおく。
とおく。
(この式の分数の方の分母に現れる
![]() は
は ![]() 以上だから割り算は常に
実行できることにも注意しておく。)
以上だから割り算は常に
実行できることにも注意しておく。)
![]() なる任意の実数
なる任意の実数 ![]() に対して、
に対して、![]() とおこう。
とおこう。
| (ア) |
と
| (イ) | 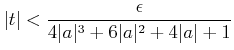 |
という2つの式が成り立つことに注意しながら以下のように計算する。
 |
||
 |
||
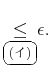 |
このことから
(2)
任意の
![]() に対して、
に対して、
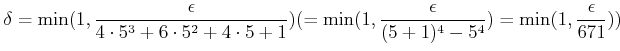
とおく。 すると、
![% latex2html id marker 850
$\displaystyle \vert f(x)-f(a)\vert {\underset{\tiny...
...xt{\ovalbox{$a\in [-5,5]$, 下記注も参照}}}{\leq }} 671 \vert t\vert <\epsilon.
$](img30.png)
(注: この不等号の左辺は正の数ばかりを足していることに注意。
当然、各項が大きいほど大きくなるので、
![]() をそれぞれ
をそれぞれ
![]() に置き換えたほうが大きくなる。)
に置き換えたほうが大きくなる。)
このことから ![]() は
は ![]() で一様連続であることが結論される。
で一様連続であることが結論される。
Next: About this document ... 2011-08-03