論理と集合要約 No.7

第7回目の主題 :

定義 7.1   集合 $X$ と $Y$ が与えられているとする。 $X$ の各元 $x$ に対して、$Y$ の元 $f(x)$ がひとつづつ与えられているとき、 $X$ から $Y$ への写像 $f$ が与えられているという。 $X$ のことを $f$ の始集合、$Y$ のことを $f$ の終集合という。

$x$ がどの元がどの元に行くかという情報とともに、 $X$ と $Y$ を指定することが大変重要である。

この状況は次のように書くと便利である。

$$f: X \to Y$$

$$\mathrel{\rotatebox[origin=c]{90}{$\in$}} \mathrel{\rotatebox[origin=c]{90}{$\in$}}$$

$$x \mapsto f(x)$$

但し、行数がかかるので、次のように一行で済ましてしまうこともある。

$$f:X \ni x \mapsto f(x) \in Y$$

いずれの表記法でも、 正しく書く習慣をつければ必ず $X,Y$ が何かまで書くことができることに 注意する。具体的には次の例を見よ。

例 7.2   つぎの各々はそれぞれ(別々の)写像である。

1. $f_\theenumi:$$\mbox{${\mathbb{R}}$}$$\ni x \to x \in$   $\mbox{${\mathbb{R}}$}$
2. $f_\theenumi:$$\mbox{${\mathbb{R}}$}$$\ni x \to x^2 \in$   $\mbox{${\mathbb{R}}$}$
3. $f_\theenumi:$$\mbox{${\mathbb{R}}$}$$_{>0} \ni x \to x^2 \in$   $\mbox{${\mathbb{R}}$}$
4. $f_\theenumi:$$\mbox{${\mathbb{R}}$}$$_{>0} \ni x \to x^2 \in$   $\mbox{${\mathbb{R}}$}$$_{>0}$
5. $f_\theenumi:{\mbox{${\mathbb{Z}}$}}\ni n \to 2 n \in \mbox{${\mathbb{R}}$}$
6. $f_\theenumi:{\mbox{${\mathbb{Z}}$}}\ni n \to 2 n \in {\mbox{${\mathbb{Z}}$}}$

対応 $x\mapsto f(x)$ についてとくに言及する必要のない場合には、 下記のように 「写像 $f:X\to Y$ 」 とか、 「 $X \overset{f}{\to} Y$ 」 と省略して書くこともある。

定義 7.3   写像 $f:X\to Y$ に対してそのグラフを

$$\Gamma_f=\{ (x,f(x)) \vert x \in X\} \subset X\times Y$$

で定義する。

問題 7.1   例 7.2 の写像のそれぞれについてそのグラフを描け。

関数をそのグラフでもって定義することもできる。

定理 7.4   集合 $X,Y$ について次のことが言える。

1. 任意の関数 $f:X\to Y$ のグラフ $\Gamma=\Gamma_f$ はつぎの性質(G)を持つ。

   性質(G)

   任意の $x_1\in X$ に対して、 「縦線集合」

   $$\{x_1\}\times Y =\{(x_1,y)\vert y \in Y\}$$

   と $\Gamma$ との共通部分はちょうどひとつの元からなる。

2. 逆に、$X\times Y$ の部分集合 $\Gamma$ が性質 (G) を持つならば、 $\Gamma$ はある一つの写像 $f:X\to Y$ のグラフである。

言い換えると、$X$ から $Y$ への写像と $X\times Y$ の特別な部分集合 を同一視することができる。この考え方をさらに一般化して、$X\times Y$ の部分集合を 与えることで $X$ から $Y$ への「対応」や、 「関係」という概念を定義することもできる。そのことについてはもっとあとで 扱おう。

解析学で言えば、連続写像、微分可能写像、代数で言えば、準同型写像のように 「...を満たす写像」を考えることは大変多いし、基本でもある。 数学を学ぶ上で、そのようなものを構成する必要が生じることも多いだろう。 そのさい、 それが写像であることをチェックするのは当然必要であるし、 場合によっては仕事の大半を占める。

問題 7.2   つぎの各々はそれぞれ写像であろうか。

1. $g_\theenumi:$   $\mbox{${\mathbb{R}}$}$$\ni x\mapsto x \in {\mbox{${\mathbb{Z}}$}}$ .
2. $g_\theenumi:$   $\mbox{${\mathbb{R}}$}$$\ni x \mapsto \sqrt{x} \in$   $\mbox{${\mathbb{R}}$}$ .
3. $g_\theenumi:$   $\mbox{${\mathbb{Q}}$}$$\ni x \mapsto ($$x$ を既約分数で書いた時の分母の絶対値$) \in {\mbox{${\mathbb{Z}}$}}$ .
4. $g_\theenumi:$   $\mbox{${\mathbb{Q}}$}$$\ni x \mapsto ($$x$ を分数で書いた時の分母$) \in {\mbox{${\mathbb{Z}}$}}$ .
5. $g_\theenumi:$   $\mbox{${\mathbb{R}}$}$$\ni x \mapsto ($$x$ を10進展開した時の小数第一位$) \in {\mbox{${\mathbb{Z}}$}}$

写像が「うまく定義されているか」否かはいかに曖昧さが排除されているかに 掛かっている場合がある。そのような場合には言葉を付け足して曖昧さを 排除することにより写像の定義を完成できることがある。

◎全射、単射、全単射。

定義 7.5   写像 $f:X\to Y$ が

1. $\forall y\in Y \exists x \in X \quad (f(x)=y)$ を満たすとき、 $f$ は全射であるという。
2. $\forall x_1,x_2 \in X (x_1\neq x_2 \implies f(x_1)\neq f(x_2))$ を満たすとき、$f$ は単射であるという。
3. 全射かつ単射であるとき、$f$ は全単射であるという。

全射、単射、全単射の判定には、$X,Y$ としてどのようなものを 考えているかが大変重要な意味を持つ。

問題 7.3   例 7.2 の各々は全射、単射、全単射であるだろうか。

グラフの言葉で言えば、次のようなことになる。

定理 7.6   写像 $f:X\to Y$ が,

1. 単射であることは、任意の $y_1\in Y$ にたいして、 $\Gamma_f$ と「横線集合」 $X\times \{y_1\}$ との共通部分がたかだか一点からなる(つまり、一点かもしくは空集合である) ことと同値である。
2. 全射であることは、任意の $y_1\in Y$ にたいして、 $\Gamma_f$ と横線集合 $X\times \{y_1\}$ との共通部分が 少なくとも一点存在すること同値である。

3. 全単射であることは、任意の $y\in Y$ にたいして、 $\Gamma_f$ と横線集合 $X\times \{y_1\}$ との共通部分が ちょうど一点存在すること同値である。

タテヨコを逆転することにより(もしくは、 簡単な論理的な議論により)、次のことが分かる。

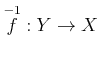定理 7.7   $f:X\to Y$ が全単射ならば、 つぎのような性質を満たす写像 $\overset{-1}{f}:Y\to X$ がただひとつ存在する。

$$y=f(x) {\Leftrightarrow} x=\overset{-1}{f}(y)$$

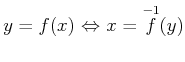
この $\overset{-1}{f}$ のことを $f$ の逆写像とよぶ。

問題 7.4   $f:$$\mbox{${\mathbb{R}}$}$$\ni x \mapsto 2 x+1 \in$   $\mbox{${\mathbb{R}}$}$ の逆写像を求めよ。