第11回目の主題 :
![]()
で定義する。
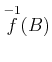 を
を
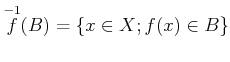
により定義する。
![]() は、「
は、「![]() の元を
の元を ![]() で送ったモノの全体」、
で送ったモノの全体」、
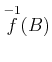 は 「
は 「![]() で送って
で送って ![]() に入るモノの全体」と唱える癖を
つけておくと扱い易い。
に入るモノの全体」と唱える癖を
つけておくと扱い易い。
![$ \overset{-1}{f}([1,2]) $](img20.png) を求めよ。
を求めよ。
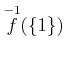 を求めよ。
を求めよ。
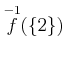 を求めよ。
を求めよ。
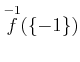 を求めよ。
を求めよ。
![$ \overset{-1}{f}([-2,-1]) $](img24.png) を求めよ。
を求めよ。
![$ \overset{-1}{f} ([1,2]\cup [3,4])$](img25.png) を求めよ。
を求めよ。
![]() は(見かけによらず)集合論的には使いやすい。
つまり、
は(見かけによらず)集合論的には使いやすい。
つまり、
![]() はさまざまな集合算と可換である。
はさまざまな集合算と可換である。
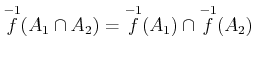 .
.
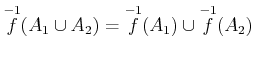 .
.
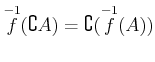 .
.
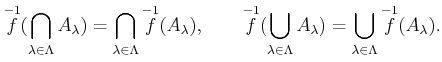
問題 11.1 で見たように、
![]() の像については逆像ほどなんでもアリ(良い性質をもつ)というわけにはいかない。
詳しくは集合論の本を見ればよいが、
さしあたっては実例が現れた時にその都度考えるぐらいで
十分だろう。
の像については逆像ほどなんでもアリ(良い性質をもつ)というわけにはいかない。
詳しくは集合論の本を見ればよいが、
さしあたっては実例が現れた時にその都度考えるぐらいで
十分だろう。
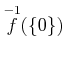 を求めよ。
を求めよ。
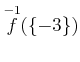 を求めよ。
を求めよ。
![$ \overset{-1}{f}([1,5])$](img48.png) を求めよ。
を求めよ。
![$ \overset{-1}{f}([3,4])$](img49.png) をもとめよ。
をもとめよ。