第12回目の主題 :
![]()
で定義する。
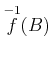 を
を
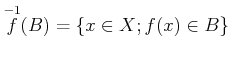
により定義する。
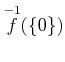 を求めよ。
を求めよ。
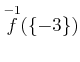 を求めよ。
を求めよ。
![$ \overset{-1}{f}([1,5])$](img17.png) を求めよ。
を求めよ。
![$ \overset{-1}{f}([3,4])$](img18.png) をもとめよ。
をもとめよ。
一般に、写像 ![]() が与えられると、
が与えられると、![]() の元は
の元は ![]() の値によって
クラス分けされる。
の値によって
クラス分けされる。
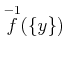 のことを
のことを 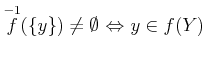 .
.
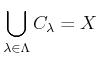 .
.
◎クラス分けと同値関係。
クラス分けは、「クラス分けの表を書く」ことにより定義することができる。 ただし、次のような難点がある。
そこで、クラス分けを定める別の方法を説明しよう。
「
![]() が同じクラスである
か同じクラスでないかのみを判定するマシン」が与えられているところを
想像すると良い。
が同じクラスである
か同じクラスでないかのみを判定するマシン」が与えられているところを
想像すると良い。
「同値関係」と、論理で言うところの「同値」とは (遠縁の親戚ぐらいにはあたるが)、別物である。よく区別すること。
か否かで判定すれば、この
とおくとき、次のことを示しなさい。
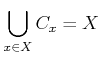 .
.
先ほどと同様に、![]() のなかから重複するものを省くことにより、
のなかから重複するものを省くことにより、
![]() のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
と定めるとき、
「ホテルヒルベルト」的な表現をしてみよう。
写像 ![]() により、
により、![]() のそれぞれの
ヒトはホテル
のそれぞれの
ヒトはホテル ![]() のある部屋に入る。
のある部屋に入る。
![]() とは、
とは、
![]() さんと
さんと ![]() さんが同じ部屋に泊まることを意味する。
入る部屋によって
さんが同じ部屋に泊まることを意味する。
入る部屋によって ![]() のクラス分けが行われるというわけである。
のクラス分けが行われるというわけである。