


Next: About this document ...
論理と集合要約 No.13
第13回目の主題 :

定義 13.1 (再)
集合
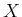
の部分集合の族
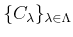
が
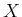
の
クラス分け (
分割とも言う)であるとは、つぎのことが成り立つときに言う。
-
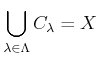 .
.
-
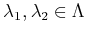 ,
,
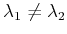 ならば
ならば
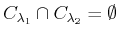 .
.
「同値関係」と、論理で言うところの「同値」とは
(遠縁の親戚ぐらいにはあたるが)、別物である。よく区別すること。
問題 13.1 (再)
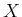
のクラス分け
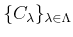
が与えられたとき、
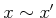
であることを
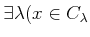
and
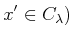
か否かで判定すれば、この
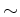
は同値関係であることを示しなさい。
問題 13.2 (再)
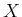
に同値関係
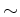
が与えられているとする。
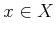
に対して、
とおくとき、次のことを示しなさい。
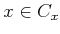 . とくに、
. とくに、
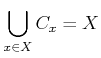 .
.
-
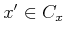
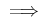
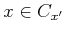 .
.
-
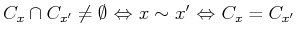 .
.
先ほどと同様に、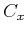 のなかから重複するものを省くことにより、
のなかから重複するものを省くことにより、
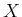 のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
定義 13.3
集合
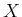
に同値関係
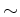
が与えられているとき、
問題
13.2 で見たように
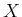
に次のようなクラス分けが定まるのであった。
このクラス分けによるクラスの全体を
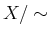
とよび、
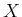
の
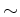
による
商集合とよぶ。
問題 13.3 (再)
写像
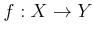
が与えられているとき、
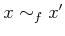
か否かの判定を
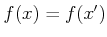
か否かでするとき、
すなわち、
と定めるとき、
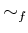
は
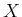
の同値関係であることを
定義に従って示しなさい。
上の問題の 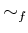 を以下でも流用する。
を以下でも流用する。



Next: About this document ...
2011-07-13
![]()
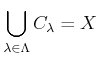 .
.
![]() のなかから重複するものを省くことにより、
のなかから重複するものを省くことにより、
![]() のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
のクラス分けを得ることができる。
容易に分かるように、上記2問題の操作は互いに逆になっている。
すなわち、クラス分けを与えることとと同値関係を与えることは
本質的に同じ事である。
![]() を以下でも流用する。
を以下でも流用する。