Next: About this document ...
代数学演習 IB 問題 No.2

注意
これからは、とくにことわらない限り、単位元をもつ環のみを扱う。「環」といえば、
単位元を持つ環と解釈していただきたい。(単位元の存在がとくに重要な時には、
一応ことわる。)ただし、積が可換であるとはまだ仮定しない。
問題 2.1
単位元
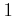
を持つ環
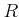
の元
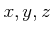
にたいして、
| |
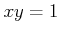 (すなわち (すなわち 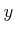 は
は 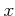 の右逆元である。)
の右逆元である。) |
|
| |
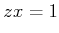 (すなわち (すなわち 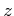 は
は 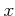 の左逆元である。)
の左逆元である。) |
|
が成り立つとき、
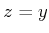
であって、
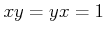
(すなわち $y(=z)$ は $x$ の逆元である)
が成り立つことを示しなさい。
定義 2.1
単位元の存在する環
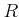
において、
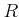
のなかで逆元が存在するような元のことを、
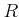
の
可逆元とか、
単元、あるいは
単数といいます。
上の条件のうち、
(1)が本質的部分であり、(2) は冒頭で述べた注意に沿うための
技術的条件である。ただし、(2)をぬかしてしまうと理論は見かけ上かなり違った
形になるので単位元のない環を扱う時(がもしあればその時)には注意が必要である。
問題 2.3
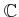
の部分環
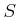
が、
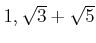
を元として持っているとします。
この時、
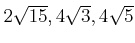
も
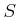
の元であることを示しなさい。
問題 2.4
有理数の全体
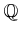
を部分環として含むような
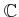
の部分環
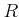
(つまり、
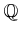
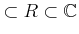
)
が
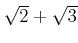
を元として含むとき、
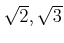
も
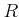
の元であることを示しなさい。
問題 2.5
有理数の全体
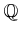
を部分環として含むような
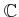
の部分環
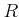
が
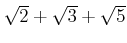
を元として含むとき、
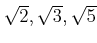
も
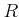
の元であることを示しなさい。
問題 2.6 (前問と同じ問題だったため削除)
問題 2.7
有理数の全体
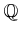
を部分環として含むような
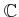
の部分環
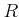
が
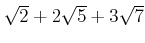
を元として含むとき、
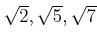
も
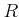
の元であることを示しなさい。
問題 2.8
有理数の全体
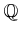
を部分環として含むような
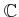
の部分環
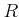
について、次の二つの条件は同値であることを
示しなさい。
-
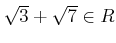 .
.
-
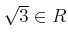 かつ
かつ
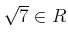 .
.
問題 2.9
前問で、
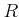
が
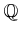
を部分環として含む、という条件を
外しても同様のことが言えるだろうか。
正しいなら証明し、間違っているなら反例を
あげなさい。
問題 2.11 (各1)
とおく。このとき、
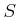 は
は
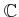 の部分環であるだろうか。
の部分環であるだろうか。
-
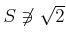 をしめしなさい。
をしめしなさい。
-
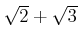 を元として含むような
を元として含むような
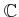 の部分環
の部分環 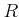 は
かならず
は
かならず 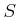 を部分集合として含むことを示しなさい。
を部分集合として含むことを示しなさい。
問題 2.12 (全部で1)
-
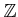 の可逆元を全て求めよ。
の可逆元を全て求めよ。
- 一般の環
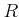 について、
について、 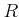 の可逆元の全体は
群をなすことを証明せよ。
の可逆元の全体は
群をなすことを証明せよ。
問題 2.13
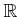
上の
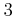
次元ベクトル空間
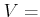
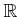
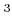
に、普通の和と、
ベクトルの外積を入れたものは環であるだろうか。
次の問題は上級者用。従って細かい説明はしない。
解こうと思うものは詳細は自分で考えること。
以下、
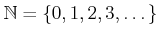 という記号を用いる。
という記号を用いる。
問題 2.14 (各1)
環
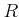
が与えられているとする。
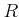
の元の列の全体
に、成分ごとの和で和を定義し、
積を
で定義するとき、
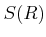 はこの和と積について環をなすことをしめしなさい。
はこの和と積について環をなすことをしめしなさい。
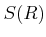 のののうち、有限数列であるものの
(すなわち、数列
のののうち、有限数列であるものの
(すなわち、数列 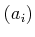 であって、
「
であって、
「
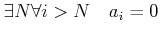 」
を満たすもの)
全体を
」
を満たすもの)
全体を 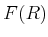 と書くと、これは
と書くと、これは 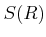 の部分環をなすことをしめしなさい。
の部分環をなすことをしめしなさい。
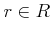 に対して、
に対して、
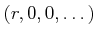 を
を 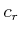 と
書くことにする。
と
書くことにする。
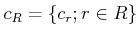 は
は 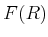 の
部分環であることを示しなさい。
の
部分環であることを示しなさい。
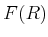 は、
は、 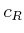 上
上
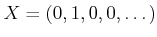 で生成されることを
示しなさい。
で生成されることを
示しなさい。



Next: About this document ...
2011-10-26
![]()
![]() という記号を用いる。
という記号を用いる。