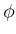 の像
の像
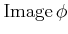 は
は 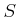 の部分環である。
の部分環である。
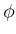 の核
の核
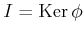 は
は 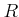 のイデアルである。
のイデアルである。
- 剰余環
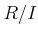 は
は
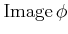 と同型である。
と同型である。
この講義の前半では、次の定理の証明を目標とする。
後半では、環や体の実例、とくに「一次元の環」 について詳しく扱う。
![]() 《環の定義・部分環の定義》
《環の定義・部分環の定義》
環とは、足し算、引き算と掛け算ができる集合のことである。
部分環とは、部分集合であって環になっているもののことである。
と掛け算と呼ばれる写像
が定義されていて次の性質を満たす時に言う。
野球の選手を集めて野球チームをつくるように、 数を集めて環を作ることができる。 環を扱う諸君はさながらチームの監督である。 「数」や「多項式」は歴史的な名プレーヤーである。 これらについては普通の和、積については結合法則や分配法則等が自動的に なりたっていることが多いのでそこはクドクド言う必要はない。
まずは「名門」チームの幾つかを知っておくべきであろう:
(2) ![]() の単位元が(見掛け上)二つあったとして、それらを
の単位元が(見掛け上)二つあったとして、それらを ![]() とおくと
とおくと
すなわち、両者は実は等しい。
環の零元と、単位元は、野球の投手と捕手と言ったところか。
ときには、チームの中の一部分が、 「特別遠征チーム」として戦わねばならないときもある:
数や行列などの、見知ったもの(名選手)を集めた集合 ![]() を作ったとする。
それが環になるか否かの判定に重要なのは、
を作ったとする。
それが環になるか否かの判定に重要なのは、
![]() には必要なメンバーが揃っているか、ということである。
つまり
には必要なメンバーが揃っているか、ということである。
つまり ![]() のなかの元を足したり、引いたり、掛けたりしたときに
のなかの元を足したり、引いたり、掛けたりしたときに
![]() のなかからはみ出す、ということがあってはならない。
そこだけ押さえれば
名選手たちなら最小限のことはしてくれる。
のなかからはみ出す、ということがあってはならない。
そこだけ押さえれば
名選手たちなら最小限のことはしてくれる。
※レポート問題
つぎのうち一問を選択して解きなさい。 (期限:次の講義の終了時まで。)
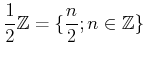
は(通常の和、積について)環ではないことを示しなさい。