Next: About this document ...

1=5 1 by -1

代数学 IB No.5要約

$\fbox{今日のテーマ}$ 《剰余環、素イデアル、極大イデアル》

前回までに、環の、そのイデアルによる剰余環について解説した。

$\displaystyle \bar{x}=\bar{y} {\Leftrightarrow}x-y \in I$

なる判定法により

にクラス分けが入ること、

に加法、乗法が代表元のとり方によらずに定まることがポイントであった。たとえば ${\mbox{${\mathbb{Z}}$}}/11 {\mbox{${\mathbb{Z}}$}}$ において、

$\displaystyle \overline{153}\times \overline{493}$

を計算するのに、 $\overline{153\times 493}$ を計算してもよいが、 $\overline{153}=\overline{-1}, \overline{493}=\overline{-2}$ と代表元を取り換えてから $\overline{-1}\times \overline{-2}$ とやっても良いわけである。

&dotfill#dotfill;

可換環と、の部分集合について、を含むのイデアルのうち最小のものを、で生成されるのイデアルといい、と表すのであった。が有限集合の場合には、 $(\{a_1,a_2,\dots,a_n\})$ のことを普通単に $(a_1,a_2,\dots,a_n)$ と書く。

補題 5.1 可換環の有限部分集合 $T=\{a_1,a_2,\dots,a_n\}$ に対して、

$\displaystyle (T)$	$\displaystyle =R a_1+R a_2+R a_3+\dots+R a_n$
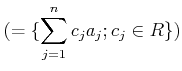	$\displaystyle (=\{\sum_{j=1}^n c_j a_j ; c_j \in R\})$

が成り立つ。

定義 5.1 可換環

の元

が

の零因子であるとは、

かつ $% latex2html id marker 1113 $ y\neq 0$$ をみたす

の元

が存在するときに言う。

定義 5.2 可換環

があたえられたとする。

に 0 以外の零因子がないなら、は整域であるという。
の 0 以外の元がで可逆であるとき、は体であるという。

もちろん、体は必ず整域である。

定義 5.3 可換環

のイデアル

( $% latex2html id marker 1147 $ R\neq I$$ )について、

が整域であるとき、はの素イデアルであるという。
が体であるとき、はの極大イデアルであるという。

これらの名前の由来はもっとあとのほうで述べる。さしあたっては、次の例が重要である。

例 5.1

${\mbox{${\mathbb{Z}}$}}$ のイデアル $\{0\}$ は ${\mbox{${\mathbb{Z}}$}}$ の素イデアルであるが、極大イデアルではない。
素数があたえられたとき、 ${\mbox{${\mathbb{Z}}$}}$ のイデアル $p {\mbox{${\mathbb{Z}}$}}$ は ${\mbox{${\mathbb{Z}}$}}$ の極大イデアルである。
正の整数が素数でないとき、 $n {\mbox{${\mathbb{Z}}$}}$ は ${\mbox{${\mathbb{Z}}$}}$ のイデアルではあるが、素イデアルではない。