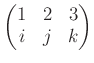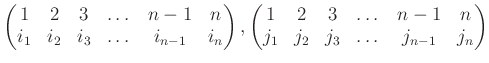Next: About this document ...
代数学 IA演習問題 No.7
 を群、
を群、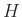 をその部分群とする。このとき、
をその部分群とする。このとき、
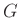 に、次のようにして同値関係
に、次のようにして同値関係 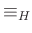 が定まります。
が定まります。
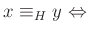
ある $h&isin#in;H$ があって、
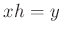
が成り立つ。
この同値関係は群論においてはとくに重要なので、
記号
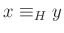 の代わりに、
の代わりに、
と書いて、
《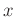 は
は 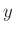 と
と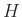 を法として左合同である》と言う事にします。
考えている
部分群
を法として左合同である》と言う事にします。
考えている
部分群 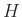 が明確なときには、「
が明確なときには、「
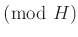 」 を書くのは省略して良いです。
」 を書くのは省略して良いです。
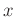 のクラス
のクラス 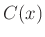 を
を 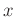 の
の 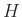 を法とする左剰余類と言います。
を法とする左剰余類と言います。
定義 7.1
上のように決めた同値関係
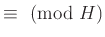
による
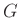
の商集合
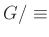
を
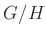
と書き、
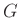
の
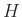
による左剰余類集合という。
問題 7.1
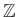
の部分群として、
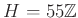
を考えます。
このとき、
となるような
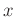
の例を5つ答えなさい。(なお、答には正の数ばかりでなく
負の数も入れること。)
定義 7.2
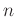
個のもの
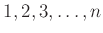
の置換全体は群になります。
この群を
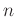
次の対称群とよび、
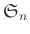
と書きます。
問題 7.3
前問で、
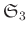
を
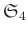
に換えて、
と置きます。このとき前問と同様な問題に答えなさい。
問題 7.4
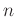
を正の整数とします。
と置きます。
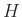 は
は
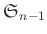 と同一視できることを示しなさい。
と同一視できることを示しなさい。
-
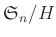 の元の個数を求めなさい。
の元の個数を求めなさい。
問題 7.6
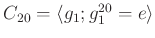
の、
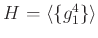
を法とする同値関係によるクラス分けを、クラス分けの表を
つくって示しなさい。
問題 7.7
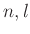
を正の整数とします。
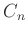
の部分群
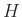
を、
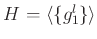
により決めます。
このとき、
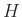
の元の個数と、左剰余類集合
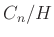
の
元の個数を求めなさい。
問題 7.8
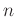
を正の整数とします。
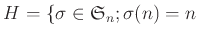
かつ
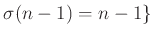
と置きます。
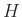 は
は
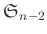 と同一視できることを示しなさい。
と同一視できることを示しなさい。
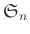 の二元
の二元
が 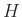 を法として同値なのはどういう時ですか?
を法として同値なのはどういう時ですか?
-
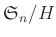 の元の個数を求めなさい。
の元の個数を求めなさい。
問題 7.9
-
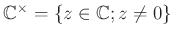 はかけ算に関して群になることを示しなさい。
はかけ算に関して群になることを示しなさい。
-
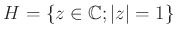 は
は
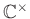 の部分群になることを示しなさい。
の部分群になることを示しなさい。
-
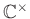 は
は 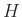 を法としてどのようにクラス分けされるか、
複素平面を利用して説明しなさい。
を法としてどのようにクラス分けされるか、
複素平面を利用して説明しなさい。
問題 7.10 (各1)
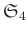
の部分群のうち、
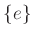
や
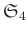
自身
以外のものを挙げなさい。ただし、単なる文字の付け替えは同じものと見なす。
問題 7.11 (各1)
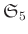
の部分群のうち、
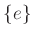
や
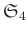
自身
以外のものを挙げなさい。ただし、単なる文字の付け替えは同じものと見なす。



Next: About this document ...
2012-05-23
![]()
![]() を群、
を群、![]() をその部分群とする。このとき、
をその部分群とする。このとき、
![]() に、次のようにして同値関係
に、次のようにして同値関係 ![]() が定まります。
が定まります。