線形代数学概論 A No.1要約

本講義の目標

ベクトル、ベクトル空間とはなにか。

定義 1.1 (記号)  

1. ${\mbox{${\mathbb{Z}}$}}$ : 整数の全体の集合
2. $\mbox{${\mathbb{Q}}$}$ : 有理数の全体の集合
3. $\mbox{${\mathbb{R}}$}$ : 実数の全体の集合
4. ${\mathbb{C}}$ : 複素数の全体の集合

全体の集合ということが大事である

定義 1.2   2次元数ベクトル

$$\mathbf a= \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}\quad ;\quad a, b \in$$   $$\mbox{${\mathbb{R}}$}$$

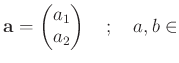
の全体の集合を2次元数ベクトル空間とよび、 $\mbox{${\mathbb{R}}$}$$^2$ と書く。

1. さしあたっては、上記のように縦ベクトルを扱うことにする。
2. ベクトルを単なる数と区別するために、高校の時のように $\vec a$ と書くこともあるし、上のように太文字で書くこともある。このテキストでは、 本講義の教科書に従い、太文字を使うことが多いだろう。

同様にして、$3$ 次元数ベクトル、$3$ 次元数ベクトル空間、 もっと一般に $n$ 次元数ベクトルと $n$ 次元数ベクトル空間が定義される。

$n$ 次元ベクトルには、成分ごとの和とスカラー倍(定数倍)により、和 と、 スカラー倍が定義される。

$n$ 次元数ベクトルとは、実数の $n$ 個の列にほかならない。 それならば、実数を無限個並べた列、すなわち実数列

$$(a_1, a_2,a_3,\dots, a_k,\dots)$$

(紙面の都合で横ベクトルで書いた。) もベクトルと考えられるのではないか。 あるいは、添字に正の整数だけを許すとかいうけち臭いことを言わずに、 もっと色々考えられるのではないか。

実はそのとおりで、それらのなす空間は無限次元ベクトル空間と呼ばれるもの になっている。

それらのベクトルを扱う際も、和と、スカラー倍のみを相手にする場合には 組織的、統一的に扱うことができる。 それが線形代数学である。言い換えると、ベクトル空間とは 和とスカラー倍の考えられるような集合のことであり、 線形代数学とは、そのような一般の線形空間を扱う学問である。

※レポート問題

(期限：次の講義の終了時まで。)

1. $$\bold a= \begin{pmatrix} 1 \\ 2 \\ 3... ... \end{pmatrix},\quad \bold b= \begin{pmatrix} 5 \\ 6 \\ 7 \\ 8 \end{pmatrix}$$
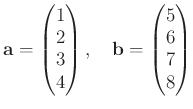
   に対して、 $\frac{1}{2}\left( \bold a + \bold b\right )$ を求めよ。

2. $\frac{1}{2}((1+ 2 x ++3 x^2+4 x^3) + (5+ 6 x +7 x~2 +8 x^3)))$ を求めよ。

3. $\frac{1}{2}\left( (\sin(x)+ 2 e^x +3 \log(x) +4 ) + (5\sin(x)+ 6 e^x +7 \log(x) +8)\right)$ を簡単にせよ。
4. ある二日間の最低気温がそれぞれ次のようであったとする。

   	Ts市	Tm 市	My市	Kc 市
   1日目	1	2	3	4
   2日目	5	6	7	8
   平均	?	?	?	?

   このとき、一日目と二日目のそれぞれの市の最低気温の平均を求めなさい。 すなわち、上の表の? の部分を埋めなさい。

● http://www.math.kochi-u.ac.jp/docky/kogi にこのプリント を提供する.