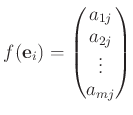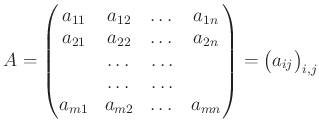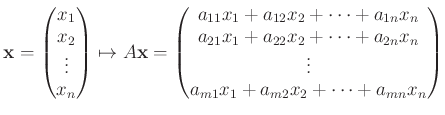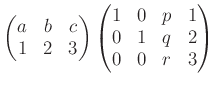Next: About this document ...
線形代数学概論 A No.4要約
 一次写像と行列。
一次写像と行列。
これ以降、係数体(スカラーの集合)としては実数体
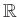 を扱います。
(が、
を扱います。
(が、
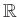 を他の体に変えてもほとんど同じことが成り立つので、余力のある人は
注意しておくとよいでしょう。)
を他の体に変えてもほとんど同じことが成り立つので、余力のある人は
注意しておくとよいでしょう。)
線形空間を比較するには線形写像を用います。
線形写像とは、和と、スカラー倍を保つような写像のことでした。
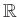
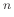 から他のベクトル空間
から他のベクトル空間 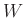 への線形写像
への線形写像 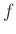 は
基本ベクトルの行き先
は
基本ベクトルの行き先
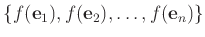 だけを決めれば定まるのでした。
だけを決めれば定まるのでした。
&dotfill#dotfill;
定義 4.1
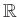
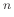
から
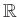

への線形写像
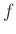
が
を満たすとき、
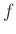
は
という数字の並びによって一意に決まる。
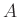
のことを
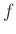
を
表現する行列
という。
(行列のサイズまで込めて言いたい時は、
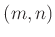
-行列とか
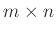
行列、
はたまた
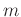
行
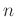
列の行列と呼ぶ。)
行列
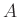
において、
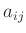
を
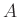
の
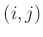
-成分、縦の数の並びを
列、
横の数の並びを
行 という。
行と列を混乱しないように覚えるには、数学のノートを思い出せば良い。
1行目、2行目、3行目etc. が第1行、第2行、第3行etc である。
見れば分かるように、線形写像(行列とベクトルの積)
は定数項のない一次式で表される。したがって、線形写像のことを一次写像
と呼ぶこともある。
命題 4.2
線形写像の合成は線形写像である。
そこで、
定義 4.2
行列の積を、対応する線形写像の合成で定義する。
具体的には、
命題 4.3
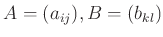 のとき
その積
のとき
その積 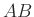 は
は
により与えられる。
※レポート問題
問題 4.1
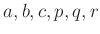
は実数とする。このとき
を計算せよ。
2012-11-16
![]() 一次写像と行列。
一次写像と行列。
![]() を扱います。
(が、
を扱います。
(が、
![]() を他の体に変えてもほとんど同じことが成り立つので、余力のある人は
注意しておくとよいでしょう。)
を他の体に変えてもほとんど同じことが成り立つので、余力のある人は
注意しておくとよいでしょう。)
![]()
![]() から他のベクトル空間
から他のベクトル空間 ![]() への線形写像
への線形写像 ![]() は
基本ベクトルの行き先
は
基本ベクトルの行き先
![]() だけを決めれば定まるのでした。
だけを決めれば定まるのでした。