行列 ![]() の分解
の分解
![]() は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
![]()
![]()
![]()
![]()
![]() の定義域
の定義域
![]()
![]() のうち、
のうち、![]() 個(の一次独立な)ベクトルが
生き残り、残りの
個(の一次独立な)ベクトルが
生き残り、残りの ![]() 個(の一次独立な)ベクトルが潰れます。
(等式
個(の一次独立な)ベクトルが潰れます。
(等式 ![]() は「次元定理」として知られています。)
は「次元定理」として知られています。)
&dotfill#dotfill;
![]()
正則行列とその逆行列。
正方行列 ![]() の逆行列を求めるには、つぎの3つの方針がある。
の逆行列を求めるには、つぎの3つの方針がある。
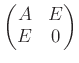 に、
上
に、
上 逆行列は連立方程式を解くのにも使える。
◎連立方程式と行基本変形。 上の例の方程式を解くには、(高校時代の言葉では)「加減法」を用いれば 良いのであった。
ここでは、(教科書に合わせて)線形方程式の基本変形という言葉を用いることにする。 じつは、線形方程式の基本変形は行列の左基本変形(行基本変形)と対応する.
例11.1のように解がひとつだけ決まるような 連立方程式は気持ちがいいが、解が複数あったり、ひとつもなかったりするような 方程式も扱う必要が生じる。 たとえば、ベクトルの一次従属性を判定するためにも必要になるのであった (No.3参照)。 具体的には、 ベクトル
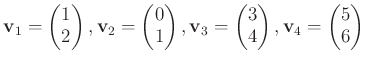
の一次従属性を判定するためには、
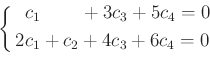
という方程式を解くのであった。
このような方程式についても、基本変形について議論できる。詳しくは次回(の予定。)
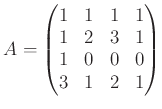
の逆行列を求めよ。行基本変形、列基本変形の いずれを用いても良いが、求め方も明記すること。
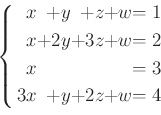
を前問の逆行列を用いてとけ。