行列 ![]() の分解
の分解
![]() は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
正則行列
は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
正則行列 ![]() の逆行列は
の逆行列は
![]() の行基本変形で求めることが
できるのでした。
の行基本変形で求めることが
できるのでした。
&dotfill#dotfill;
![]()
連立一次方程式と基本変形
一般に、
![]()
![]()
![]() に対して
に対して
![]() となるような
となるような ![]() の全体を
の全体を
![]() の核といい、
の核といい、
![]() で表す。
で表す。
![]() の核は
の核は
![]()
![]() の線形部分空間であることが
容易に分かる。行列の核は行列を調べる際に基本になる。
の線形部分空間であることが
容易に分かる。行列の核は行列を調べる際に基本になる。
![]() の核を求めるのは斉次型(つまり、定数項のない)連立一次方程式
の核を求めるのは斉次型(つまり、定数項のない)連立一次方程式
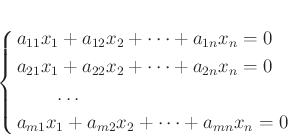
を解くのと同じことである。
(※) 転置行列。
行列
![]()
![]()
![]() の行と列をひっくり返してできる行列、
すなわち
の行と列をひっくり返してできる行列、
すなわち
![]() のことを
のことを ![]() の転置行列といい、
の転置行列といい、![]() で書き表す。
たとえば、
で書き表す。
たとえば、
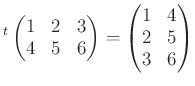
などという具合。 転置行列は次の性質を持つ
(
| 行 | 列 | |||
| 行列を左から掛ける | 行列を右から掛ける | |||
| 左基本変形 | 右基本変形 |
◎(非斉次)連立一次方程式 一般に、 連立方程式
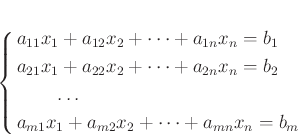
を解くことを考えよう。これは、
という方程式を解くのと同じことである。 行列
という行列を考えると少しだけ便利である。(変数を書くのがサボれる。)この行列のことを上の方程式の 拡大係数行列と 呼ぶ。
今回は上の方程式を行基本変形のみを用いて解いてみよう。
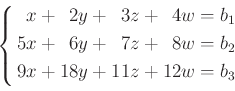
を解いてみよう。拡大係数行列は 行基本変形を行うと、次のような具合になる。
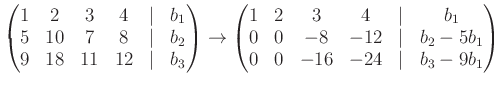 |
||
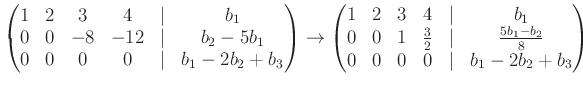 |
最後の行列は階段行列になっている。
行基本変形ではここらあたりまでしか変形できないが、
方程式の解を求めるにはこれでも間に合う。
すなわち、与えられた方程式は
![]() が成り立つ場合にのみ解を持ち、
その場合の解は
(「階段」の角にあたる
が成り立つ場合にのみ解を持ち、
その場合の解は
(「階段」の角にあたる![]() の係数の
の係数の ![]() を他の変数で芋づる式に
表すことにより、)
を他の変数で芋づる式に
表すことにより、)
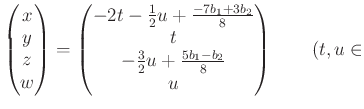
である。
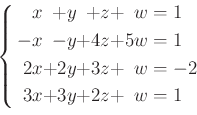
を拡大係数行列の行基本変形を利用してとけ。