Commutative algebra

Yoshifumi Tsuchimoto

DEFINITION 03.1   For any commutative ring $A$ , we define its spectrum as

$$\operatorname{Spec}(A)=\{ \mathfrak{p}\subset A; \mathfrak{p}$$ is a prime ideal of $A$$$.$$

For any subset $S$ of $A$ we define

$$V(S)=V_{\operatorname{Spec}A} (S) =\{\mathfrak{p}\in \operatorname{Spec}A; \mathfrak{p}\supset S\}$$

Then we may topologize $\operatorname{Spec}(A)$ in such a way that the closed sets are sets of the form $V(S)$ for some $S$ . Namely,

$$F:$$closed$$\iff \exists S \subset A ( F=V(S) )$$

We refer to the topology as the Zariski topology.

LEMMA 03.2   For any ring $A$ , the following facts holds.

1. For any subset $S$ of $A$ , we have
   $$V(S)=\bigcap_{s \in S} V(\{s\}).$$

2. For any subset $S$ of $A$ , let us denote by $\langle S \rangle$ the ideal of $A$ generated by $S$ . then we have
   $$V(S)=V(\langle S \rangle)$$

PROPOSITION 03.3   For any ring homomorphism $\varphi: A \to B$ , we have a map

$$\operatorname{Spec}(\varphi): \operatorname{Spec}(B) \ni \mathfrak{p}\mapsto \varphi^{-1}(\mathfrak{p})\in \operatorname{Spec}(A).$$

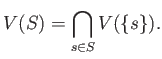
It is continuous with respect to the Zariski topology.

PROPOSITION 03.4   For any ring $A$ , the following statements hold.

1. For any ideal $I$ of $A$ , let us denote by $\pi_I :A\to A/I$ the canonical projection. Then $\operatorname{Spec}(\pi_I)$ gives a homeomorphism between $\operatorname{Spec}(A/I)$ and $V_{\operatorname{Spec}A}(I)$ .
2. For any element $s$ of $A$ , let us denote by $\iota_s: A \to A[s^{-1}]$ be the canonical map. Then $\operatorname{Spec}(\iota_s)$ gives a homeomorphism between $\operatorname{Spec}(A[s^{-1}])$ and $\complement V_{\operatorname{Spec}_A}(\{s\})$ .

PROPOSITION 03.5   Let $A,B$ be a ring. Let $\varphi: A \to B$ be a ring homomoprhism. We regard $B$ as an $A$ module via $\varphi.$ If $B$ is a finite $A$ -module, then

$$\operatorname{Spec}(\varphi): \operatorname{Spec}(B)\to \operatorname{Spec}(A)$$

is a closed map with respect to the Zariski topology.

DEFINITION 03.6   Let $X$ be a topological space. A closed set $F$ of $X$ is said to be reducible if there exist closed sets $F_1$ and $F_2$ such that

$$F=F_1 \cup F_2,\quad F_1\neq F, F_2 \neq F$$

holds. $F$ is said to be irreducible if it is not reducible.

DEFINITION 03.7   Let $I$ be an ideal of a ring $A$ . Then we define its radical to be

$$\sqrt{I}=\{ x \in A; \exists N\in \mathbb{Z}_{>0}$$    such that $$x^N \in I\}.$$

PROPOSITION 03.8   Let $A$ be a ring. Then;

1. For any ideal $I$ of $A$ , we have $V(I)=V(\sqrt{I})$ .
2. For two ideals $I$ , $J$ of $A$ , $V(I)=V(J)$ holds if and only if $\sqrt{I}=\sqrt{J}$ .
3. For an ideal $I$ of $A$ , $V(I)$ is irreducible if and only if $\sqrt{I}$ is a prime ideal.

DEFINITION 03.9   We define a dimension of a topological space $X$ as a supremum of the length of sequences

$$Y_1 \supsetneq Y_2 \supsetneq Y_3 \supsetneq \dots \supsetneq Y_s$$

of irreducible subsets of $X$ .

We define the Krull dimension of a ring $A$ as the dimension of $\operatorname{Spec}(A)$ .