


Next: About this document ...
Commutative algebra
Yoshifumi Tsuchimoto
Let
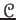 be an abelian category. For any object
be an abelian category. For any object 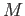 of
of
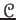 ,
the extension group
,
the extension group
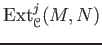 is defined to be the derived functor of
the ``hom'' functor
is defined to be the derived functor of
the ``hom'' functor
We note that the
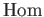 functor is a ``bifunctor''.
We may thus consider the right derived functor of
functor is a ``bifunctor''.
We may thus consider the right derived functor of
 and that of
and that of
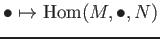 .
Fortunately, both coincide:
The extension group
.
Fortunately, both coincide:
The extension group
 may be calculated by using either an
injective resolution of the second variable
may be calculated by using either an
injective resolution of the second variable 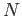 or
a projective resoltuion of the first variable
or
a projective resoltuion of the first variable 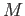 .
.
EXAMPLE 09.1
Let us compute the extension groups
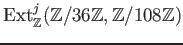
.
- We may compute them by using an injective resolution
of
 .
.
- We may compute them by using a free resolution
of
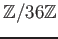 .
.
EXERCISE 09.1
Compute an extension group
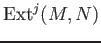
for modules
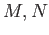
of your choice.
(Please choose a non-trivial example).
DEFINITION 09.2
Let
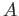
be an associative unital (but not necessarily commutative) ring.
Let
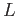
be a right
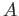
-module. Let
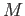
be a left
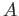
-module.
For any (
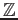
-)module
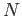
, an map
is called an
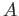 -balanced biadditive map
-balanced biadditive map if
-
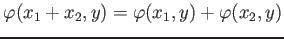
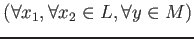 .
.
-
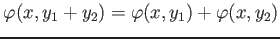
 .
.
-
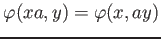
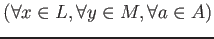 .
.
DEFINITION 09.4
We employ the assumption of the proposition above.
By a standard argument on universal objects, we see that such object is
unique up to a unique isomorphism. We call it
the
tensor product of
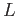
and
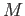
and denote it by
DEFINITION 09.6
For any left
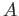
-module
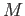
,
the left derived functor
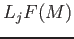
of
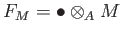
is called the Tor functor
and denoted by
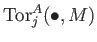
.
By definition,
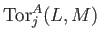 may be computed by using projective resolutions of
may be computed by using projective resolutions of 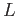 .
.
EXERCISE 09.2
Compute
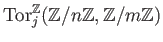
for
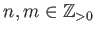
.



Next: About this document ...
2012-06-28
![]() be an abelian category. For any object
be an abelian category. For any object ![]() of
of
![]() ,
the extension group
,
the extension group
![]() is defined to be the derived functor of
the ``hom'' functor
is defined to be the derived functor of
the ``hom'' functor
![]() functor is a ``bifunctor''.
We may thus consider the right derived functor of
functor is a ``bifunctor''.
We may thus consider the right derived functor of
![]() and that of
and that of
![]() .
Fortunately, both coincide:
The extension group
.
Fortunately, both coincide:
The extension group
![]() may be calculated by using either an
injective resolution of the second variable
may be calculated by using either an
injective resolution of the second variable ![]() or
a projective resoltuion of the first variable
or
a projective resoltuion of the first variable ![]() .
.
![]() may be computed by using projective resolutions of
may be computed by using projective resolutions of ![]() .
.