代数学 IA No.1要約

一学期の目標

定理 1.1 (群の準同型定理)   群 $G$ から別の群 $H$ への準同型写像 $\phi:G\to H$ が与えられたとする。 このとき、次が成り立つ。

1. $\phi$ の像 $\operatorname{Image}\phi$ は $H$ の部分群である。
2. $\phi$ の核 $N=\operatorname{Ker}\phi$ は $G$ の部分群である。
3. 剰余群 $G/N$ は $\operatorname{Image}\phi$ と同型である。

群とはなにか。

群とは、操作の集まりである。ルービックキューブの操作などが良い例である。

ただし、次のような条件を付ける。

• 操作は、必ず元に戻せる。
• 操作を２つ続けて行うことができる。 (操作 $a,b$ に対して、その２つを続けて行う操作を $a$ と $b$ の合成と呼び、 $a \circ b$ などと書く。)

便宜上、もうひとつ「何もしないのもひとつの操作と呼ぶ」という条件 を付け加えておく。

大事な事が２つ:

• 許される操作の集まりをあらかじめ指定しておくことが大事である。
• 操作の手順を「書かれたとおり」に行えば、 誰でも同じ操作を実現できる。

じつは「合成」のなかまとして、「加える」ことや「掛ける」ことを考えることも できる。これらを総称して「演算」と呼ぶことにし、 数学的にきちんとした言葉で書くと、次のようになる。

定義 1.1 (群の定義)   集合 $G$ が群であるとは、

(群0)「演算」と呼ばれる写像 $G\times G\ni(x,y) \mapsto x \circ y\in G$ が定義されていて、

次の条件を満たすときに言う。

(群1).

その演算は結合法則を満たす。

$$(x\circ y) \circ z =x \circ (y\circ z) \quad (\forall x,y,z \in G)$$

(群2).

$G$ には単位元(普通 $e$ と書かれる)が存在する。すなわち、 ある $G$ の元 $e$ があって、

$$e \circ x=x, \quad x \circ e=x \quad (\forall x \in G)$$

がなり立つ。

(群3).

$G$ の各元には逆元がある。すなわち、$G$ の任意の元 $x$ に対して、 $G$ のある元 $y$ が存在して、

$$x \circ y=e,\quad y \circ x=e$$

がなりたつ。

群の定義において、集合 $G$ を決めただけではどんな演算を考えているのか 明確でないので、正確には、組 $(G,\circ)$ を群と呼ぶ。

上の定義を満たすものなら、どんなものでも群である。 このようなものを十把一絡げに扱ってしまうのが群論の一般論である。

例 1.1   次の $(G,\circ)$ はそれぞれ群である。

1. $G={\mbox{${\mathbb{Z}}$}}$ , $x \circ y=x+y$ . (この群のことを ${\mbox{${\mathbb{Z}}$}}$ の加法群 $({\mbox{${\mathbb{Z}}$}},+)$ と呼ぶ。)
2. $G=$$\mbox{${\mathbb{Q}}$}$$\setminus \{0\}$ , $x\circ y=xy$ . ( $\mbox{${\mathbb{Q}}$}$ の 乗法群 $($$\mbox{${\mathbb{Q}}$}$$^{\times} ,\times)$ と呼ぶ。)
3. $G={\operatorname{GL}}_n($$\mbox{${\mathbb{R}}$}$$)$ , $x\circ y=xy$ .
4. 正三角形 $\Delta$ を自分自身に重ね合わせる操作の全体 $\mathbb{D}_3$ .

上の最後の例については、置換により表現することができる。 $\Delta$ の頂点 $\{1,2,3\}$ がどの頂点に行くかを書くことにより、 $\mathbb{D}_3$ の元を記述できるのである。

$$\mathbb{D}_3=\{ \begin{pmatrix} 1 2 3 \\ 1 2 3 \end{pma... ...1 2 \end{pmatrix}, \begin{pmatrix} 1 2 3 \\ 3 2 1 \end{pmatrix}\}$$

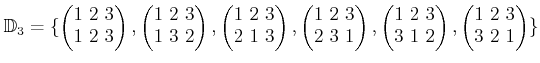
巡回置換を使った表記を使えば、もっと簡単に記述できる。 ルービックキューブなども同様に取り扱える。 慣れるまで馴染みにくいかもしれないが、手軽にノートに書いて操作を扱えるのは 大きな利点である。

例 1.2   次の $(G,\circ)$ はそれぞれ群でない。

1. $G=\mathbb{N}$ , $x \circ y=x+y$ .
2. $G=$$\mbox{${\mathbb{Q}}$}$ , $x\circ y=xy$ .
3. $G={\operatorname{GL}}_n($$\mbox{${\mathbb{R}}$}$$)$ , $x \circ y=x+y$ .

$\bullet$ 写像、全射、単射、全単射の復習

写像 $f:X\to Y$ が、

1. 全射であるとは、どんな $Y$ の元 $y$ を取ってきても、$f(x)=y$ の解 $x\in X$ が存在するときに言う
2. 単射であるとは、$x_1,x_2$ が $X$ の異なる二つの元のときには、いつでも $f(x_1)\neq f(x_2)$ がなり立つときに言う。
3. 全単射であるというのは、全射でかつ単射のときに言う。

写像のことを話すときには始集合 $X$ 、終集合 $Y$ を 明確にしておくことが大事である。

例 1.3   数 $x$ に対してその二乗 $x^2$ を対応させる写像 $f$ を考える。 始集合、終集合をいろいろ変えてみることを考えてみよう。

1. $f:$$\mbox{${\mathbb{R}}$}$$\to$   $\mbox{${\mathbb{R}}$}$ 全射でも単射でもない。
2. $f:$$\mbox{${\mathbb{R}}$}$$_{>0}\to$   $\mbox{${\mathbb{R}}$}$ 単射であるが全射でない。
3. $f:$$\mbox{${\mathbb{R}}$}$$\to$   $\mbox{${\mathbb{R}}$}$$_{\geq 0}$ 全射であるが単射でない。
4. $f:$$\mbox{${\mathbb{R}}$}$$_{>0}\to$   $\mbox{${\mathbb{R}}$}$$_{>0}$ 全単射である。

$\bullet$ デカルト積集合の復習

集合 $A,B$ のデカルト積集合 $A\times B$ とは、 $A$ の元と $B$ の元との組全体のなす集合である。すなわち、

$$A\times B=\{(a,b);a\in A,\quad b\in B\}$$

例えば、

$$\{0,1,2\} \times \{a,b\} = \{ (0,a),(0,b), (1,a),(1,b), (2,a),(2,b) \}$$

$$\{0,1\} \times \{0,1\} = \{(0,0),(0,1),(1,0),(1,1)\}$$

※レポート問題

次の中から一問を選んで、レポートとして提出しなさい。

(期限：次の講義の終了時まで。)

(I).

${\mbox{${\mathbb{Z}}$}}\setminus \{-100\}$ は加法に関して群をなすだろうか、 理由を挙げて述べなさい。

(II).

${\mbox{${\mathbb{Z}}$}}$ に、演算 $\circ$ を

$$x \circ y=x+y+3$$

で定義する。このとき、 $({\mbox{${\mathbb{Z}}$}},\circ )$ は群であるか、理由をつけて答えなさい。

● http://www.math.kochi-u.ac.jp/docky/kogi にこのプリント を提供する.