群とは操作の集まりでした。演算が定義されるということ、 (つまり、演算について閉じていること)、 「何もしない」という操作、各操作の逆操作がその集まりに含まれるという事 が大事なのでした。
![]() 《有限群》
《有限群》
![]() 元の数が有限であるような群を、有限群と言う。
元の数が有限であるような群を、有限群と言う。
![]() 群
群 ![]() の元の個数を、
の元の個数を、![]() の位数と言い、
の位数と言い、![]() で表す。
で表す。
有限群の重要な例として、有限対称群、有限巡回群、二面体群がある。
置換
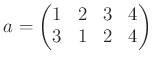
は、
というようにも書く。
二つの置換の結合(演算)は通常《後ろから読》む。たとえば、
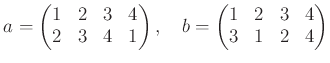
の掛け算
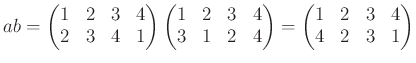
つまり、例えば
いくつかの元
![]() を順繰りに変える置換、すなわち
を順繰りに変える置換、すなわち
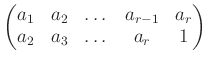
のことを 巡回置換と呼び、
「一つの元から生成されていて、元の数が有限である巡回群を、 有限巡回群という」というのが正統的な定義なのだが、 ここでは「生成する」の定義を後回しにして、 つぎのような間に合わせな的な定義をしておくことにする。
を位数
注意
上の元 ![]() について、
について、
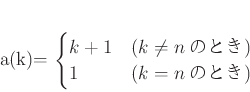
と書ける。だが、場合分けをするより、もっと楽な方法がある。
以上のようにしておいて、
![]() は
は
![]() の置換だとみなすと、
の置換だとみなすと、
と書ける。これは以後の定理の証明に非常に有効である。
が成り立つということと、
![]() のなかで、
のなかで、
![]() と、
と、
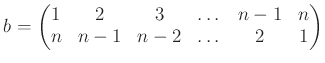
とで生成された群を
注意
等式
が成り立つ。 さらに、 先ほど述べた
が成り立つ。
の
※レポート問題
次の中から一問を選んで、レポートとして提出しなさい。
(期限:次の講義の終了時まで。)