群とは、操作の集まりでした。群をうまく扱うためには、
適当な「同一視」を行うと便利な場合があるのでした。
ルービックキューブがそれなりに汚れてきても面の色の揃い方だけで区別したり、
正 ![]() 角形の頂点に複数の名前を与えて、
角形の頂点に複数の名前を与えて、
![]() は
は
![]() が
が ![]() の倍数の時にする。等です。
の倍数の時にする。等です。
![]() 《同値関係》
《同値関係》
![]() 《同値関係》と《クラス分け》とは一つの現象を裏と表とから眺めたものである。
《同値関係》と《クラス分け》とは一つの現象を裏と表とから眺めたものである。
集合に同値関係を入れるということは、集合のクラス分けをする事と同じことになる。クラス分けの正確な定義は、次のようになる。
がなりたつ。
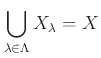
がなりたつ。(各
| (※) |
により、同値関係が定まり、
レポート問題
(I)
日常生活に現れる簡単な集合 ![]() とその上の同値関係
とその上の同値関係 ![]() の例をあげ、その例において
の例をあげ、その例において ![]() がどのようなものであるか
述べよ。
(条件の設定の仕方によっては同値関係と呼べるかどうか
怪しいものもある。そのようなものについては、どこが弱点か、
どのようにすれば改善するかも述べること。)
がどのようなものであるか
述べよ。
(条件の設定の仕方によっては同値関係と呼べるかどうか
怪しいものもある。そのようなものについては、どこが弱点か、
どのようにすれば改善するかも述べること。)