


Next: About this document ...
1=7
代数学 IA No.7要約
群を考えるときは同一視がついてまわるのでした。
同一視は、同値関係によるクラス分けを用いることで語ることができるのでした。
 《群の、部分群による左剰余類集合》
《群の、部分群による左剰余類集合》
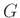 を群、
を群、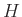 をその部分群とする。このとき、
をその部分群とする。このとき、
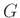 に、次のようにして同値関係
に、次のようにして同値関係 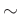 が定まる。
が定まる。
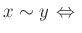
ある $h&isin#in;H$ があって、
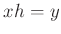
が成り立つ。
定理 7.1
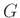 を群、
を群、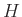 をその部分群とする。このとき、
をその部分群とする。このとき、
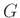 に、次のようにして同値関係
に、次のようにして同値関係 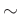 が定まる。
が定まる。
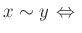
ある $h&isin#in;H$ があって、
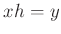
が成り立つ。
これからはこの同値関係には記号 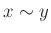 の代わりに、
の代わりに、
と書いて、《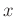 は
は 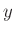 と
と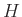 を法として左合同である》と言う事にする。考えている 部分群
を法として左合同である》と言う事にする。考えている 部分群 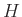 が明確なときには、
が明確なときには、
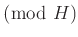 を書くのは省略して良い。
を書くのは省略して良い。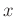 のクラス
のクラス 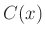 を
を 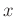 の
の 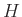 を法とする左剰余類と言う。
を法とする左剰余類と言う。
 上のように決めた同値関係
上のように決めた同値関係
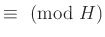 による
による 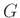 の商集合
の商集合
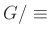 を
を 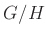 と書き、
と書き、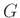 の
の 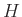 による左剰余類集合という。
による左剰余類集合という。
例 7.1
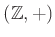
をその部分群
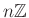
で割ると、以前に説明した
「拡張した番号づけをされた頂点の集合」 と同じものが
得られる。
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
- 元
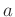 で生成される位数二十の有限巡回群
で生成される位数二十の有限巡回群
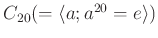 を考えます。
を考えます。
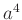 で生成される
で生成される 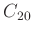 の部分群
の部分群 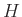 の元をすべて書き出し、
の元をすべて書き出し、
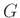 が、《
が、《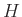 を法として左合同》と言う同値関係でどのように類別されるか、
を法として左合同》と言う同値関係でどのように類別されるか、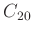 の元のクラス分けの表を作って示しなさい。特に、
の元のクラス分けの表を作って示しなさい。特に、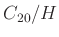 の元の個数はいくらか?
の元の個数はいくらか?
- (II).
- 群
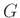 とその部分群
とその部分群 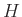 とが与えられたとします。
とが与えられたとします。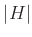 と
と 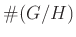 とが
ともに有限ならば、
とが
ともに有限ならば、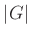 も有限である事を示しなさい。
も有限である事を示しなさい。



Next: About this document ...
2012-07-12
![]() 《群の、部分群による左剰余類集合》
《群の、部分群による左剰余類集合》
![]() を群、
を群、![]() をその部分群とする。このとき、
をその部分群とする。このとき、
![]()
![]() に、次のようにして同値関係
に、次のようにして同値関係 ![]() が定まる。
が定まる。
![]() の代わりに、
の代わりに、![]() 上のように決めた同値関係
上のように決めた同値関係
![]() による
による ![]() の商集合
の商集合
![]() を
を ![]() と書き、
と書き、![]() の
の ![]() による左剰余類集合という。
による左剰余類集合という。