


Next: About this document ...
代数学 IA No.8要約
群 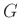 の部分群
の部分群 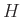 が与えられると、
が与えられると、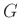 自体のクラス分けが定まるのでした。
自体のクラス分けが定まるのでした。
&dotfill#dotfill;
 《群の、部分群による左剰余類集合は、いつ群になるか。》
《群の、部分群による左剰余類集合は、いつ群になるか。》
群の部分群による剰余集合が、「自然なやり方で」群になるには、
その部分群が正規部分群である事を仮定するのが良い。
定義 8.1
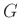
を群、
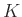
をその部分群とする。
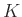
が
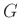
の正規部分群であるとは、
任意の
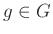
と任意の
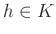
とに対して、
が成り立つときに言う。
定理 8.3
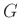 を群、
を群、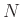 をその正規部分群とする。このとき
をその正規部分群とする。このとき 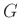 の二つの元
の二つの元 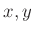 に関する次の二つの条件は同値である。
に関する次の二つの条件は同値である。
- (1).
- ある
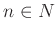 があって、
があって、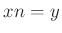 が成り立つ。
が成り立つ。
- (2).
- ある
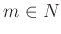 があって、
があって、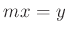 が成り立つ。
が成り立つ。
すなわち、正規部分群でクラスわけする時には、
「左」「右」をあまり気にしなくて良い。
発展
※レポート問題
つぎのうち一問を選択して解きなさい。
(期限:次の講義の終了時まで。)
- (I).
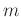 を正の整数とします。二面体群
を正の整数とします。二面体群
の、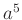 で生成された部分群を求めなさい。さらに、これが
で生成された部分群を求めなさい。さらに、これが
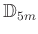 の正規部分群であるかどうかを調べなさい。
の正規部分群であるかどうかを調べなさい。
- (II).
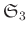 の、
の、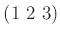 で生成された部分群をここでは仮に
で生成された部分群をここでは仮に 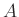 と書くことにします。
と書くことにします。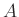 は、
は、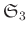 の正規部分群であることを示しなさい。さらに、
の正規部分群であることを示しなさい。さらに、
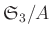 はどのような群になるか、かけ算の表をつくって答えなさい。
はどのような群になるか、かけ算の表をつくって答えなさい。
- (III).
- 《発展》に挙げた定理のうち、
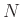 が正規部分群であると言う部分の証明を書きなさい。
(ヒント:次のステップの各々に説明をつければ良い。どれも「明らか」ではない。(もちろん他のやり方を考えてもよろしい。)
が正規部分群であると言う部分の証明を書きなさい。
(ヒント:次のステップの各々に説明をつければ良い。どれも「明らか」ではない。(もちろん他のやり方を考えてもよろしい。)
-
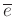 は
は 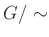 の単位元である。
の単位元である。
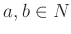 ならば
ならば 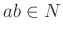 .(サービス:
.(サービス: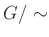 の乗法が代表元の取りかたによらない事から、
の乗法が代表元の取りかたによらない事から、
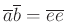 でなければならない。)
でなければならない。)
-
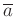 の
の 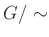 での逆元は
での逆元は
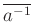 である。
である。
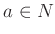 ならば
ならば
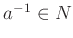 .
.
-
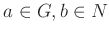 ならば
ならば
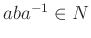 .
.



Next: About this document ...
2012-07-12
![]() の部分群
の部分群 ![]() が与えられると、
が与えられると、![]() 自体のクラス分けが定まるのでした。
自体のクラス分けが定まるのでした。
![]() 《群の、部分群による左剰余類集合は、いつ群になるか。》
《群の、部分群による左剰余類集合は、いつ群になるか。》
