


Next: About this document ...
代数学 IA No.13要約
 群の直積 (+準同型定理の応用)
群の直積 (+準同型定理の応用)
定義 13.1 (群の直積)
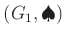
と、
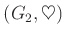
とが共に群であるとする。このとき、デカルト積集合
は、次のような演算
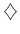
により群になる。
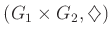
を
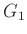
と
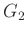
の(群としての)直積と呼ぶ。
定理 13.1 (有限巡回群の直積分解)
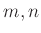 を互いに素な正の整数とする。このとき、同型
を互いに素な正の整数とする。このとき、同型
が存在する。
系 13.1
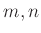 を互いに素な整数とすると、
を互いに素な整数とすると、
となる整数 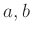 が存在する。
が存在する。
この系自身もよく利用される。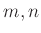 が具体的に与えられたとき、
が具体的に与えられたとき、
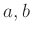 の値を具体的に求めるには、ユークリッドの互除法を用いると良い。
応用例として一つだけ挙げておく。
の値を具体的に求めるには、ユークリッドの互除法を用いると良い。
応用例として一つだけ挙げておく。
※レポート問題
- (I).
-
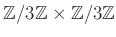 は 巡回群ではないことを証明しなさい。
は 巡回群ではないことを証明しなさい。
2012-07-23
![]() 群の直積 (+準同型定理の応用)
群の直積 (+準同型定理の応用)