論理と集合要約 No.8

写像は始集合と終集合をコミにして考える必要があるのでした。 合コンのメンツが大事なように、 $X$ と $Y$ にどのぐらいの元があるのかが重要です。 このことをうまく用いて、写像は始集合と終集合との元の多さを比べるのにも 使われます。

&dotfill#dotfill;

第8回目の主題 :

◎全射、単射、全単射。

定義 8.1 (再)   写像 $f:X\to Y$ が

1. $\forall y\in Y \exists x \in X \quad (f(x)=y)$ を満たすとき、 $f$ は全射であるという。
2. $\forall x_1,x_2 \in X (x_1\neq x_2 \implies f(x_1)\neq f(x_2))$ を満たすとき、$f$ は単射であるという。
3. 全射かつ単射であるとき、$f$ は全単射であるという。

全射、単射、全単射の判定には、$X,Y$ としてどのようなものを 考えているかが大変重要な意味を持つ。

定理 8.2 (再)   写像 $f:X\to Y$ が,

1. 単射であることは、任意の $y_1\in Y$ にたいして、 $\Gamma_f$ と「横線集合」 $X\times \{y_1\}$ との共通部分がたかだか一点からなる(つまり、一点かもしくは空集合である) ことと同値である。
2. 全射であることは、任意の $y_1\in Y$ にたいして、 $\Gamma_f$ と横線集合 $X\times \{y_1\}$ との共通部分が 少なくとも一点存在すること同値である。

3. 全単射であることは、任意の $y\in Y$ にたいして、 $\Gamma_f$ と横線集合 $X\times \{y_1\}$ との共通部分が ちょうど一点存在すること同値である。

定理 8.3 (再)   $f:X\to Y$ が全単射ならば、 つぎのような性質を満たす写像 $f^{-1}:Y\to X$ がただひとつ存在する。

$$y=f(x) \ {\Leftrightarrow}\ x={f}^{-1}(y)$$

この $f^{-1}$ のことを $f$ の逆写像とよぶ。

問題 8.1 (再)   $f:$$\mbox{${\mathbb{R}}$}$$\ni x \mapsto 2 x+1 \in$   $\mbox{${\mathbb{R}}$}$ の逆写像を求めよ。

◎写像と直積の関係。

直積の定義を思い出すと、次のことがわかる。

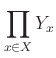
定理 8.4   集合 $X$ , $Y$ が与えられているとする。$X$ のおのおのの元 $x$ に対して $Y$ のコピー $Y_x$ を用意すれば、 $\{ Y_x\}_{x \in X}$ はひとつの集合の族である。 $X$ から $Y$ への写像 $f$ は

$$\prod_{x \in X} Y_x$$

の元 $(f(x))_{x \in X}$ と同一視される。すなわち、 直積集合 $\prod_{x \in X} Y_x$ は$X$ から $Y$ への写像全体の集合と同一視できる。

いちいち $Y$ のコピーなどというのは煩わしいので、 次のような記号を用いるときもある。

定義 8.5   $X$ から $Y$ への写像の全体のなす集合を $Y^X$ と書く。これはまた

$$\operatorname{Hom}_{\text{set}} (X,Y)$$

と書く場合もある。

別の見方をすれば、集合の族 $\{X_\lambda\}$ の直積

$$\prod_{\lambda \in \Lambda } X_\lambda$$

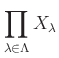
は写像の集合(写像空間)の拡張概念だとも言える。

次のことは選択公理と呼ばれる事実である。

公理 8.6   空でない集合ばかリからなる集合族 $\{X_\lambda\}_{\lambda \in \Lambda}$ に たいして、 $\prod_\lambda X_\lambda$ は空ではない。 言い換えると、無限個の空でない集合たち $X_\lambda$ から、いっせいに一つづつ 元を取り出すことが可能である。

◎「ホテルヒルベルト」

一般に、 $X$ から $Y$ への単射が存在することは、 $X$ の元のほうが $Y$ の元よりも「少ない」ことを意味すると考えられる。 $X$ の各々の元を「人」、$Y$ の各々の元を「ホテルの部屋」に例えると、 単射の存在は一人ひとりが別々の部屋に入れることを意味するからである。 ただし、無限集合においては、「多い」「少ない」の感覚は有限集合とは 少し異なる。

問題 8.2   つぎのことをそれぞれ示しなさい。

1. ${\mbox{${\mathbb{Z}}$}}_{>0}$ から ${\mbox{${\mathbb{Z}}$}}_{>0}\setminus \{1\}$ への全単射が存在する。
2. ${\mbox{${\mathbb{Z}}$}}$ から $2 {\mbox{${\mathbb{Z}}$}}$ への全単射が存在する。
3. ${\mbox{${\mathbb{Z}}$}}$ から ${\mbox{${\mathbb{Z}}$}}_{>0}$ への単射が存在する。
4. ${\mbox{${\mathbb{Z}}$}}_{>0}^2$ から ${\mbox{${\mathbb{Z}}$}}$ への単射が存在する。
5. ${\mbox{${\mathbb{Z}}$}}^2$ から ${\mbox{${\mathbb{Z}}$}}$ への単射が存在する。
6. 任意の整数 $n$ にたいして、 ${\mbox{${\mathbb{Z}}$}}^n$ から ${\mbox{${\mathbb{Z}}$}}$ への単射が存在する。
7. $\mbox{${\mathbb{Q}}$}$ から ${\mbox{${\mathbb{Z}}$}}$ への単射が存在する。

定義 8.7   集合 $A$ に対して、$A$ の濃度と呼ばれる記号 $\char93 A$ を定める。 濃度の間の等号は、次のような意味で使う。

$$\char93 A = \char93 B\ {\Leftrightarrow}\$$    ($A$ から $B$ への全単射が存在する。)

この定義もちょっと間に合わせ的である。(あとで「同値関係」 という概念を導入することによりすこしマシにできる。)

定義 8.8   集合 $A$ から $B$ への単射が存在するとき、 $\char93 A \leq \char93 B$ と 書くことにする。

この定義は $A,B$ のとり方によらず、$A,B$ の濃度のみで決まっている。

定理 8.9   集合 $A,B,C$ に対して、

$$(\char93 A \leq \char93 B$$$$\text { and } \char93 B \leq \char93 C ) \implies \char93 A \leq \char93 C$$

がなりたつ。

つぎの定理は面白いが、証明は少し難しいので集合算についてもう少し述べてから 時間があれば証明することにする。

定理 8.10 (ベルンシュタイン)  

$$(\char93 A \leq \char93 B$$$$\text { and } \char93 B \leq \char93 A ) \implies \char93 A =\char93 B$$

がなりたつ。

濃度の言葉(とベルンシュタインの定理)を用いると、次のことが分かる

$$\char93 {\mbox{${\mathbb{Z}}$}}= \char93 ({\mbox{${\mathbb{Z}}$... ...mathbb{Q}}$}=\char93 \mbox{${\mathbb{Q}}$}^2=\char93 \mbox{${\mathbb{Q}}$}^3$$