![]() 行列の演算。単位行列。ゼロ行列。
行列の演算。単位行列。ゼロ行列。
行列の計算(和、差、積、スカラー倍)は普通の数を計算するのと同じように計算できる。
但し、次のことだけが通常の数と異なるので注意を要する。
正の整数 ![]() にたいして、
にたいして、![]() 行列の全体
行列の全体
![]()
![]()
![]() のことを、
のことを、
![]()
![]()
![]() と書く。
と書く。
![]()
![]()
![]() の元同士はは、いつでも足したり、引いたり、
掛けたりできる。
の元同士はは、いつでも足したり、引いたり、
掛けたりできる。
◎単位行列
![]()
![]() から
から
![]()
![]() への恒等写像
への恒等写像
![]() は線形写像である。
対応する行列は
は線形写像である。
対応する行列は
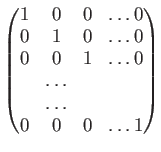
と、対角に
◎ゼロ行列
![]()
![]() の任意の元
の任意の元
![]() にたいし、
にたいし、
![]()
![]() の元
の元 ![]() (ゼロベクトル)
を対応する写像は線形写像である。
対応する行列は
(ゼロベクトル)
を対応する写像は線形写像である。
対応する行列は
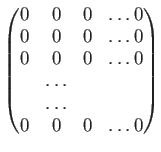
と、すべての成分が 0 であるような行列である。これをゼロ行列と言い、
単位行列は ![]() の、ゼロ行列は 0
の役割を果たす。
の、ゼロ行列は 0
の役割を果たす。
◎行列単位
![]() 成分のみが
成分のみが ![]() で、あとはすべて 0
であるような行列のことを、
行列単位といい、
で、あとはすべて 0
であるような行列のことを、
行列単位といい、![]() で書き表す。
で書き表す。
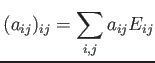
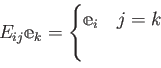
◎クロネッカーのデルタ。
次のような記号を用いると便利であることが多い。 (クロネッカーのデルタ)
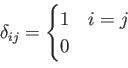
これを用いると、
と、場合分けをいちいち書かずに済む。
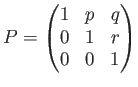
を行列単位
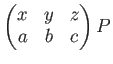
を計算しなさい。