行列 は 普通の数のように、足したり引いたり掛けたりできるのでした。 サイズに気をつけること、積が可環ではないことに注意が必要でした。
&dotfill#dotfill;
![]() 行列のブロック区分け
行列のブロック区分け
行列をいくつかのブロックに分けて考えることができる。 上手に使えば計算が簡単になる。本日の問題1 を参照のこと
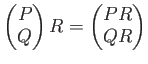
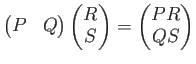
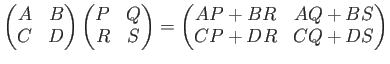
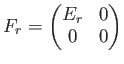
◎行列のべき乗、逆行列。
ブロック区分けの威力を知るために、 いくつか言葉を用意しておくことにする。 「逆行列」についてはあとでもっと組織的に研究することになる。
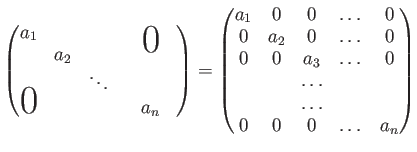
のことを 対角行列という。
上の命題は、ブロック対角化されたような行列についても拡張される。
を満たすもののことを、
![]() の逆行列が存在するとき、
の逆行列が存在するとき、
![]() ,
,
![]() ,
,
![]() ,
, ![]() を
を
![]() と
書く。(ついでに、
と
書く。(ついでに、![]() と書く。) 通常の数と同じように
と書く。) 通常の数と同じように
が
問題が複数あるときにはそのどれか1問を解くこと。
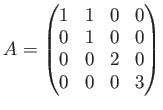
とおく。
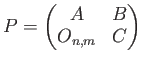 の逆行列を
の逆行列を
![]() を用いて求めよ。
を用いて求めよ。
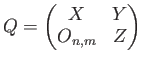 と仮定して、
と仮定して、
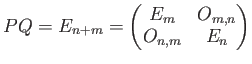 を満たすという条件から
を満たすという条件から