行列 ![]() の分解
の分解
![]() は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
正則行列
は
「どのベクトルを活かすか」、「どのベクトルは潰すか」を
決めていると考えることができるのでした。
正則行列 ![]() の逆行列は
の逆行列は
![]() の行基本変形で求めることが
できるのでした。
の行基本変形で求めることが
できるのでした。
&dotfill#dotfill;
![]()
連立一次方程式と基本変形(2)
両側基本変形を用いると、一次方程式の解法は大変見通しが良くなる。
| (あ) |
を得たとする。 このとき、
と書いてみると、
| (い) |
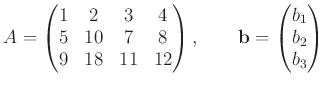
のときを考えよう。
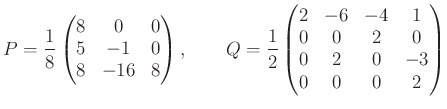
により、
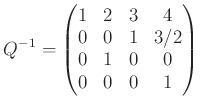
と変数変換すれば、
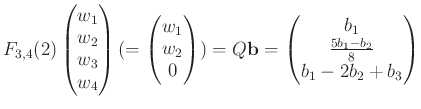
をとけば良いことになる。それは易しい。
◎一般逆行列。
与えられた 行列
![]()
![]()
![]() に対して、
に対して、
![]()
![]()
![]() で、
で、
を満たすようなものを
一般逆行列は一意ではない。 が、
一般逆行列を用いて連立方程式を求めることもできる。
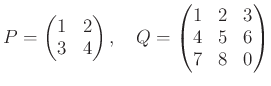
とおく。 さらに、
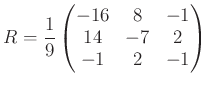
とおく。
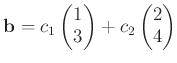 と書いた時、
方程式(※) が解を持つためには、
と書いた時、
方程式(※) が解を持つためには、