DEFINITION 4.3
Let
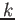
be a field.
- We put
and call it (the set of 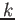 -valued points of) the projective space.
The class of an element
-valued points of) the projective space.
The class of an element
 in
in 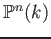 is
denoted by
is
denoted by
![$ [x_0:x_1:\dots:x_n]$](img16.png) .
.
- Let
![$ f_1,f_2,\dots, f_l \in k[X_0,\dots, X_n]$](img17.png) be homogenious polynomials. Then we set
be homogenious polynomials. Then we set
and call it (the set of 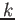 -valued point of) the projective variety
defined by
-valued point of) the projective variety
defined by
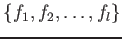 .
.
(Note that the condition
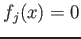
does not depend on the choice of the
representative
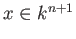
of
![$ [x]\in \P ^n(k)$](img22.png)
.)
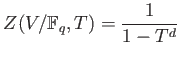
![]()