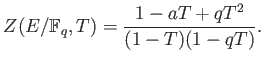Next: Bibliography
Zeta functions. No.5
Yoshifumi Tsuchimoto
We quote the famous

It is a profound theorem, relating rational points
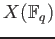 of
of 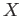 over finite fields
and topology of
over finite fields
and topology of
 .
.
The following proposition (which is a precursor of the above conjecture)
is a special case
PROPOSITION 5.2 (Weil)
Let 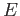 be an elliptic curve over
be an elliptic curve over
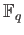 . Then we have
. Then we have
where 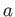 is an integer which satisfies
is an integer which satisfies
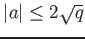 .
.
Note that for each 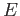 we have only one unknown integer
we have only one unknown integer 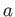 to
determine the Zeta function. So it is enough to compute
to
determine the Zeta function. So it is enough to compute
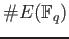 .
to compute the Zeta function of
.
to compute the Zeta function of 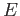 . (When
. (When 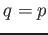 then one may use
the result in the preceding section.)
then one may use
the result in the preceding section.)
For a further study we recommend [1, Appendix C],[2].



Next: Bibliography
2013-07-15
![]()
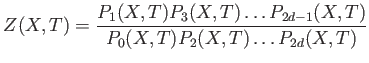
![]() of
of ![]() over finite fields
and topology of
over finite fields
and topology of
![]() .
.