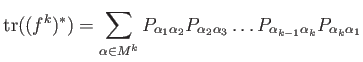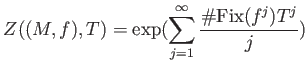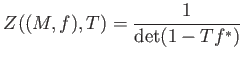Yoshifumi Tsuchimoto
Let ![]() be a self map
be a self map ![]() of a set
of a set ![]() .
It defines a (discrete) dynamical system
.
It defines a (discrete) dynamical system ![]() .
.
To explain the basic idea, we first examine the case where ![]() is a
finite set.
is a
finite set.
We put
![]() , the set of
, the set of
![]() -valued functions on
-valued functions on ![]() .
.
![]() defines a pull-back of functions:
defines a pull-back of functions:
and push-forward:
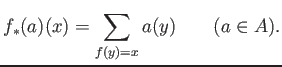
(It might be better to treat the push-forward as above as a push-forward of measures.)
We note also that any element of ![]() admits an integration
admits an integration
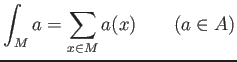
(which is a integration with respect to the counting measure.)
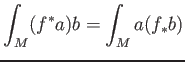
In other words,