Yoshifumi Tsuchimoto
Congruent zeta as a zeta of a dynamical system.
The definition of Artin Mazur zeta function is valid without
assuming the number of the base space ![]() to be a finite set.
to be a finite set.
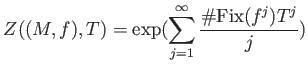
Let ![]() be a power of a prime
be a power of a prime ![]() .
We may consider an automorphism
.
We may consider an automorphism
![]() of
of
![]() over
over
![]() by
by
For any projective variety ![]() defined over
defined over
![]() ,
we may define a Frobenius action
,
we may define a Frobenius action
![]() on
on
![]() :
:
For any
![]() -valued point
-valued point
![]() , We have
, We have