


Next: About this document ...
代数学II要約 No.12
今日のテーマ:

環 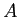 と有限群
と有限群 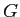 が与えられているとき、
群環
が与えられているとき、
群環 ![$ A[G]$](img4.png) が定義される。
実は、
が定義される。
実は、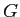 は
は ![$ A[G]$](img4.png) 自体の上に表現できる。
このことを、とくに
自体の上に表現できる。
このことを、とくに 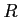 が体
が体 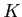 のときに詳しく見てみることにする。
のときに詳しく見てみることにする。
定義 12.1
環
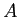
と群
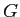
が与えられたとき、
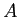
上の
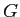
の
群環 ![$ A[G]$](img4.png)
とは、
形式的な有限和の集合
に形式的に和、積を導入したものである。
(「
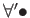 」 は「有限個の例外を除いて全ての
」 は「有限個の例外を除いて全ての  に対して」
という意味である。)
に対して」
という意味である。)
具体的には、和、積は次のように与えられる。
-
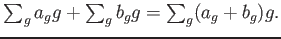
-
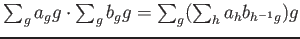
定義 12.2
体
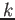
が与えられているとする。群
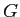
の
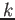
上の
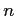
-次線形表現
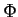
とは、群準同型
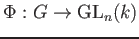
の
ことである。
命題 12.3
群
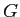
の
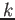
上の
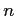
-次線形表現
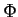
が与えられたとき、
![$ A[G]$](img4.png)
の
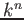
への作用が
で定まる。
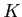 上の
上の 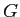 の
の 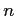 -次元表現
-次元表現 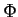 が決まると、
が決まると、
![$ K[G]$](img18.png) の
の 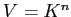 への作用が命題3.6 のように定まって、
への作用が命題3.6 のように定まって、
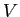 は
は ![$ K[G]$](img18.png) -加群の構造を持つ。逆に、
-加群の構造を持つ。逆に、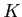 -上有限次元の
-上有限次元の ![$ K[G]$](img18.png) -加群
-加群 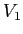 が与えられれば、(すなわち、
が与えられれば、(すなわち、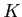 -ベクトル空間
-ベクトル空間 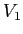 上に
上に
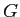 の作用が定まっていれば、)
その基底を固定することにより、
の作用が定まっていれば、)
その基底を固定することにより、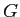 の表現が定まることが
容易に分かる。
行列を書くよりもその方が簡明であることが多いので、
以下では多くの場合
の表現が定まることが
容易に分かる。
行列を書くよりもその方が簡明であることが多いので、
以下では多くの場合 ![$ K[G]$](img18.png) の作用でもって表現を定義する。
の作用でもって表現を定義する。
補題 12.4
有限群
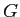
と体
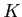
が与えられているとする。
![$ K[G]$](img18.png)
自身は
![$ K[G]$](img18.png)
上の左加群と
みなすことができる。
この表現
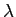
を
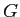
の左正則表現と呼ぶ。
厳密にいえば、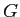 の元にどのように順番を付けるかによって
の元にどのように順番を付けるかによって
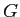 の各元を表す行列は違ってくる。
ここでは
の各元を表す行列は違ってくる。
ここでは 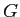 の元の順番は適当に付けて、それを明示した上で行列で表現する
ことにする。
の元の順番は適当に付けて、それを明示した上で行列で表現する
ことにする。
問題 12.1
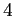
つの元の偶置換全体のなす群
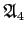
の正則表現で、
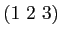
および
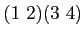
に対応する行列を書き下しなさい。
(
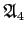
の元の順番を明示しておくこと。)
問題 12.2
位数
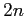
の二面体群
の正則表現で、
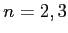
の場合(できれば、もっと一般の場合も)
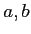
に対応する行列はどのようになるか答えなさい。
(二面体群については、すでに二年生段階で習っているはずなので、本問では詳しくは
述べない。)
2013-07-11
![]()
![]() と有限群
と有限群 ![]() が与えられているとき、
群環
が与えられているとき、
群環 ![]() が定義される。
実は、
が定義される。
実は、![]() は
は ![]() 自体の上に表現できる。
このことを、とくに
自体の上に表現できる。
このことを、とくに ![]() が体
が体 ![]() のときに詳しく見てみることにする。
のときに詳しく見てみることにする。
![% latex2html id marker 852
$\displaystyle A[G]=
\left\{
\sum_{g \in G} a_g g \ ; \qquad a_g=0 \quad \forall' g \in G
\right\}
$](img7.png)
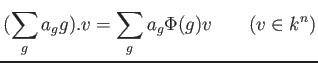
![]() 上の
上の ![]() の
の ![]() -次元表現
-次元表現 ![]() が決まると、
が決まると、
![]() の
の ![]() への作用が命題3.6 のように定まって、
への作用が命題3.6 のように定まって、
![]() は
は ![]() -加群の構造を持つ。逆に、
-加群の構造を持つ。逆に、![]() -上有限次元の
-上有限次元の ![]() -加群
-加群 ![]() が与えられれば、(すなわち、
が与えられれば、(すなわち、![]() -ベクトル空間
-ベクトル空間 ![]() 上に
上に
![]() の作用が定まっていれば、)
その基底を固定することにより、
の作用が定まっていれば、)
その基底を固定することにより、![]() の表現が定まることが
容易に分かる。
行列を書くよりもその方が簡明であることが多いので、
以下では多くの場合
の表現が定まることが
容易に分かる。
行列を書くよりもその方が簡明であることが多いので、
以下では多くの場合 ![]() の作用でもって表現を定義する。
の作用でもって表現を定義する。