第4回目の主題 :
![]()
まずは論理の復習
論理復習ここまで
集合の関係を論理で述べることもよくある。
は正しいだろうか?
集合と論理とは裏腹の関係にあるのであった。論理の ![]() や
や ![]() に対応する集合論的な概念も存在する。
に対応する集合論的な概念も存在する。
同様に、集合 ![]() の一つ一つの元
の一つ一つの元 ![]() に対して集合
に対して集合 ![]() が与えられたとき、集合の族
が与えられたとき、集合の族
![]() が与え
られたという。
が与え
られたという。![]() のことをこの族の添字集合と呼ぶ。
のことをこの族の添字集合と呼ぶ。
もちろん集合列は集合族の特別な場合である。
![]() のことを
のことを
![]() のように書いているのである。
のように書いているのである。
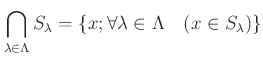
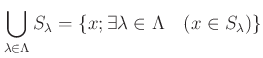
により定義する。
集合列については、その共通部分
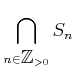
のことを
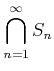
のごとく書くことも多い。和集合も同様。
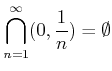
であることを示しなさい。 右辺の記号は空集合といって、元をひとつも持たない集合のことをさす 記号である。
![$\displaystyle \bigcap_{\epsilon>0} (-\infty, 1+\epsilon) =(-\infty, 1]
$](img25.png)
であることを示しなさい。 左辺は堅苦しく書けば
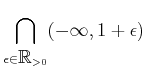 となるところであるが、上のように省略することが往々にしてある。
となるところであるが、上のように省略することが往々にしてある。
論理と集合の裏腹の関係をうまく利用して、論理的な事柄を 集合算で表現してさまざまな役に立つ集合を作ることができる。 位相空間論と測度論の最初のところなどはとくにその手法が顕著に現れる。
例として、 次のようなことを考えよう。
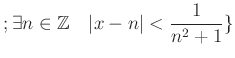 |
||
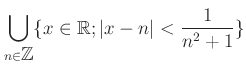 |
||
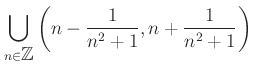 |
この集合は、長さの総和 ![]() が有限 (
が有限 (
![]() )
であるような開区間の和集合であり、
)
であるような開区間の和集合であり、
![]() を部分集合として含んでいる。
を部分集合として含んでいる。
同様にして、任意の
![]() に対して、
に対して、
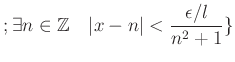 |
||
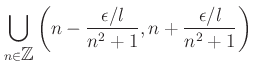 |
![% latex2html id marker 1267
$\displaystyle \{ x \in [0,1] ; \forall n \in {\mbo...
... \in {\mbox{${\mathbb{Z}}$}} \quad (\vert\frac{m}{n} -x\vert<\frac{1}{n^3})) \}$](img41.png) |
||
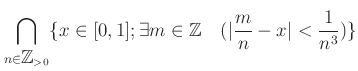 |
||
![$\displaystyle \bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{m \in {\mbox{${\mathbb{Z}}$}}} \{ x \in [0,1] : \vert\frac{m}{n} -x\vert<\frac{1}{n^3} \}$](img43.png) |
||
![$\displaystyle \bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{m \in {\mbo...
...[0,1] \cap \big( \frac{m}{n} -\frac{1}{n^3}, \frac{m}{n} +\frac{1}{n^3} \big) )$](img44.png) |
||
![$\displaystyle [0,1]\cap (\bigcap_{n \in {\mbox{${\mathbb{Z}}$}}_{>0}} \bigcup_{...
...bb{Z}}$}}} \big( \frac{m}{n} -\frac{1}{n^3}, \frac{m}{n} +\frac{1}{n^3} \big) )$](img45.png) |
このことは、実は、
![]()
![]() が長さの総和が有限の開区間の和集合で
覆えることを表している。
が長さの総和が有限の開区間の和集合で
覆えることを表している。