


Next: About this document ...
代数学III要約 No.5
今日のテーマ:

今回は少しガロア理論の本筋からは外れる。
これまで、個々の例の多項式の既約性について証明なしに議論してきたが、
だんだん不自由になってきたのでここでまとめておくことにする。
代数についてよく学びたい人のための注:
今回の議論は
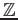 とその商体
とその商体
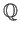 に関してのべるが、
一般の UFD
に関してのべるが、
一般の UFD 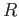 とその商体
とその商体 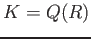 に関しても同様なことが成り立つ。
に関しても同様なことが成り立つ。
次の命題は多項式の既約性判定の際に整数係数と有理係数の差を
うまく処理してくれる:
命題 5.1
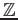
上の多項式
![$ f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img6.png)
が
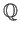
上で可約ならば、
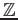
上でも可約である。
証明には「ガウスの補題」を用いる。その説明のために
ひとつ言葉を用意しておこう。
定義 5.2
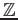
上の多項式
![$ f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img6.png)
が
原始的であるとは
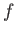
の係数のすべてを割るような整数が
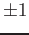
しかないときにいう。
言い換えると、原始的多項式とは係数の gcd が
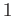
の多項式である。
補題 5.3 (ガウス)
原始多項式
![$ f,g\in {\mbox{${\mathbb{Z}}$}}[X]$](img10.png)
の積
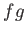
はまた原始的である。
命題 5.5
体
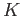
上の
3次もしくは2次の多項式
![$ f\in K[X]$](img17.png)
について、
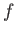
が
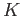
の中に根を持たなければ
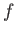
は
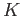
上既約である。
定理 5.6 (アイゼンシュタイン)
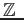
を係数にもつモニックな
が、ある素数 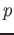 に対して、次の二つの性質をもつとする。
に対して、次の二つの性質をもつとする。
-
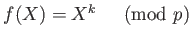
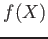 の定数項は
の定数項は 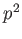 で割り切れない。
で割り切れない。
このとき、
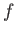
は
上既約である。
次のこともよく用いる。
定理 5.7
任意の
![$ f\in k[X]$](img25.png)
と任意の定数
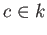
に対して、
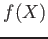 が既約
が既約
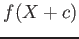 が既約.
が既約.
定理 5.8
モニックな整係数多項式
![$ f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img6.png)
が与えられているとする。
ある素数
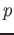
に対して
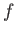
が
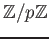
係数の多項式として既約なら、
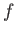
は
![$ [X]$](img30.png)
の元として既約で
ある。
問題 5.1
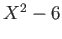
は
上既約であることを示しなさい。
(今回はもちろん 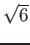 が無理数であることを使ってはならない。)
が無理数であることを使ってはならない。)
問題 5.2
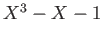
は
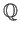
上既約であることを示しなさい。



Next: About this document ...
2013-10-31
![]()
![]() とその商体
とその商体
![]() に関してのべるが、
一般の UFD
に関してのべるが、
一般の UFD ![]() とその商体
とその商体 ![]() に関しても同様なことが成り立つ。
に関しても同様なことが成り立つ。
![]() に対して、次の二つの性質をもつとする。
に対して、次の二つの性質をもつとする。
![]() が既約
が既約
![]()
![]() が既約.
が既約.