


Next: About this document ...
代数学III要約 No.11
例題
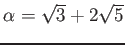 ,
,
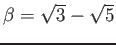 とおくとき、
とおくとき、
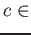
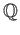 ,
,
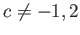 ならば
ならば
[証明]
次のステップで証明する。
-
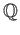
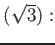
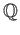
![$ ]=2. $](img11.png)
-
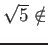
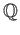

-
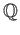
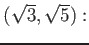
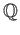
![% latex2html id marker 976
$ (\sqrt{3})]=2$](img15.png) .
.
-
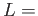
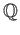
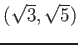 は
は
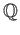 のガロア拡大であって、
その拡大次数は
のガロア拡大であって、
その拡大次数は 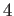 .
.
-

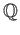
 の元
の元 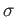 は
は 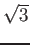 の行き先
の行き先
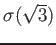 (
(
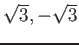 の二通り。)
と
の二通り。)
と 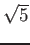 の行き先
の行き先
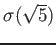 (
(
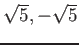 の二通り)
により定まる。しかも、それら (
の二通り)
により定まる。しかも、それら (
 ) 4通りの組み合わせは
すべてガロア群の元
として現れる。
) 4通りの組み合わせは
すべてガロア群の元
として現れる。
-
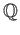
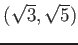 の
の
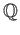 ベクトル空間としての基底として
ベクトル空間としての基底として
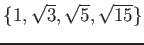 を取ることができる。
を取ることができる。
-
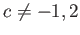 なら、 ガロア群
なら、 ガロア群

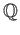
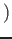 の元で、
の元で、
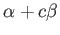 を動かさないものは、
ガロア群の単位元(恒等写像)に限る。
を動かさないものは、
ガロア群の単位元(恒等写像)に限る。
上のように、
ガロア理論を知った上でなら、次の補題の内容が分かりやすくなる。
(この補題自体は、ガロア理論の構築そのものに必要であったので、
ガロアの基本定理(ガロア対応)を用いずに証明する必要があった。)
補題 11.1 (補題6.8再掲)
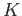
は無限個の元を持つ体とする。
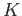
上の代数的な元
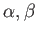
が、ともに
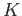
上分離的ならば
をみたす
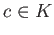
が少なくともひとつ存在する。
二重根号について。
次のような等式がある。
つまり、
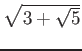 は 右辺のように簡単化できる。
これを二重根号をはずすという。
同様に、次のような等式が成り立つことがわかる。
は 右辺のように簡単化できる。
これを二重根号をはずすという。
同様に、次のような等式が成り立つことがわかる。
一方で、
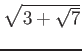 は上のようには簡単にならない。
これは、次のように説明できる。
は上のようには簡単にならない。
これは、次のように説明できる。
-
 のガロア拡大
のガロア拡大  で、
で、
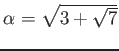 を
元として含むものは、
を
元として含むものは、
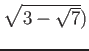 も元として含む。
も元として含む。
-
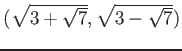 .
.
-
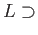
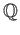
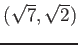 .
.
-
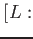
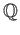
![% latex2html id marker 1064
$ (\sqrt{7},\sqrt{2})]=2$](img48.png) .
.
- もし、
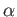 が有理数
が有理数 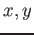 でもって
でもって
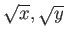 の有理係数の有理式としてかけるなら、
の有理係数の有理式としてかけるなら、
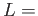
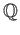
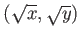 と
なって、上の事実と矛盾する。
と
なって、上の事実と矛盾する。
2014-01-16
![]() ,
,
![]() とおくとき、
とおくとき、
![]()
![]() ,
,
![]() ならば
ならば
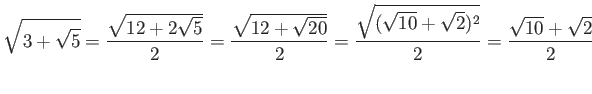
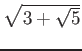 は 右辺のように簡単化できる。
これを二重根号をはずすという。
同様に、次のような等式が成り立つことがわかる。
は 右辺のように簡単化できる。
これを二重根号をはずすという。
同様に、次のような等式が成り立つことがわかる。
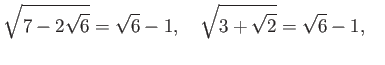
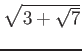 は上のようには簡単にならない。
これは、次のように説明できる。
は上のようには簡単にならない。
これは、次のように説明できる。
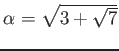 を
元として含むものは、
を
元として含むものは、
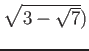 も元として含む。
も元として含む。
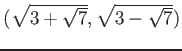 .
.