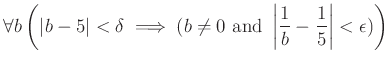![]()
![]()
がなりたつときにいう。
極限の定義により、上の定義は次のように言い換えられる。
![]()
上の定理は「定理」ではあるが、
連続性の定義における ``![]() '' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理のほうを用いて判定することにする。実際には、関数
'' の「例外的な扱い」を取り除いてむしろ
自然な形をしている。そこでこの講義ではもっぱら連続性を確かめるには
上の定理のほうを用いて判定することにする。実際には、関数 ![]() が
が
![]() の近くで定義されているという前提条件は強すぎる。そこで
定義域についての条件をハッキリ記述して次のように定義しよう。
の近くで定義されているという前提条件は強すぎる。そこで
定義域についての条件をハッキリ記述して次のように定義しよう。
(☆)
![]()
を満たすときに言う。
![]() を明示することにより、
を明示することにより、![]() の動く範囲に関する制限が明確になる。
とくに
の動く範囲に関する制限が明確になる。
とくに ![]() が
が
![]() のときを考えれば「右連続性」
が自然に解釈できる。
のときを考えれば「右連続性」
が自然に解釈できる。