


Next: About this document ...
微分積分学概論AI要約 No.11

定義 11.1
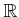
の部分集合
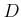
上で定義された
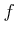
が
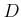
で連続であるとは、その定義域の全ての点
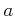
で連続であること、すなわち、
が成り立つときに言う。
上の定理は、下の定理の多変数版を用いるともっと鮮やかに証明される
定理 11.3
二つの連続関数の合成関数は連続である。
次のことは、「連続 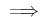 グラフがつながっている」ということの
表現法の一つと言える。
グラフがつながっている」ということの
表現法の一つと言える。
定理 11.5 (``教科書定理14'', 中間値の定理)
関数
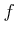
が閉区間
![$ [a,b]$](img15.png)
で連続(すなわち、
![$ [a,b]$](img15.png)
の各点で連続)とする。
このとき
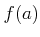
と
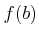
の中間の値
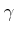
にたいして、
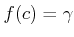
をみたすような
![$ c\in [a,b]$](img20.png)
が存在する。
上の定理は、位相空間論において「連結集合の連続像は連結である」という
定理に一般化される。
(区間は実数直線の連結部分集合として特徴づけることができる。)
2011-06-17
![]()
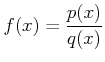 ($p,q$ は $x$ の多項式)
($p,q$ は $x$ の多項式)
![]() グラフがつながっている」ということの
表現法の一つと言える。
グラフがつながっている」ということの
表現法の一つと言える。