第11回目の主題 :
![]()
で定義する。
により定義する。
![]() は、「
は、「![]() の元を
の元を ![]() で送ったモノの全体」、
で送ったモノの全体」、
![]() は 「
は 「![]() で送って
で送って ![]() に入るモノの全体」と唱える癖を
つけておくと扱い易い。
に入るモノの全体」と唱える癖を
つけておくと扱い易い。
![]() は(見かけによらず)集合論的には使いやすい。
つまり、
は(見かけによらず)集合論的には使いやすい。
つまり、![]() はさまざまな集合算と可換である。
はさまざまな集合算と可換である。
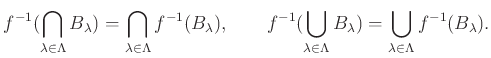
![]() の像については一部の集合算と可換ではない。
詳しくは集合論の本を見ればよいが、
さしあたっては実例が現れた時にその都度考えるぐらいで
十分だろう。次の諸問題も参照のこと。
の像については一部の集合算と可換ではない。
詳しくは集合論の本を見ればよいが、
さしあたっては実例が現れた時にその都度考えるぐらいで
十分だろう。次の諸問題も参照のこと。
![]() (
(![]() を
を ![]() で割った余り)
で割った余り)
で定義する。このとき、