Yoshifumi Tsuchimoto
From the paper of Encinas and Hauser:
&dotfill#dotfill;
The coefficient ideal of an ideal ![]() of
of ![]() at a with respect to
at a with respect to
![]() is an ideal in
is an ideal in ![]() which is built from the coefficients of the Taylor expansion
of the elements of
which is built from the coefficients of the Taylor expansion
of the elements of ![]() with respect to the equations defining
with respect to the equations defining ![]() .
Let
.
Let ![]() and
and ![]() be regular systems of parameters of
be regular systems of parameters of
![]() and
and
![]() so that
so that ![]() defines
defines ![]() in
in ![]() .
For
.
For ![]() in
in ![]() denote by
denote by
![]() the
elements of
the
elements of
![]() so that
so that
![]() holds after passage to the completion.
Then we set
holds after passage to the completion.
Then we set
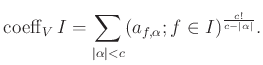
&dotfill#dotfill;
Let us choose
Let ![]() be a closed subscheme of a regular scheme
be a closed subscheme of a regular scheme ![]() .
We want to resolve the singularity of
.
We want to resolve the singularity of ![]() .
If there exists an regular hypersurface
.
If there exists an regular hypersurface ![]() such that
such that
![]() ,
then we may replace
,
then we may replace ![]() by
by ![]() . So we may (have to) assume that
. So we may (have to) assume that
![]() is not contained in such hypersurfaces.
Instead, we have for each point
is not contained in such hypersurfaces.
Instead, we have for each point ![]() a
``hypersurface of maximal contact''
a
``hypersurface of maximal contact'' ![]() .
.
![]() is not canonical, but is good enough to define the invariant
is not canonical, but is good enough to define the invariant ![]() and then (afterwards) determine the center of blow up.
and then (afterwards) determine the center of blow up.