Next: About this document ...
代数学演習 I 問題 No.8
今回(No.8)は、「環」と言えば単位元を持つ可換環のことを指すことにします。また、「準同型」は単位元を保つものだけを考えることにします。
問題 8.2
一般に、体
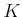
上の一次式
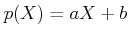
(
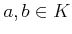
,
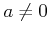
) に対して、
![$ K[X]/(p(X)) \cong K$](img11.png)
であることを示しなさい。
問題 8.3
前問で、
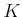
が体であるという仮定をやめて
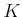
が一般の可換環であると
仮定した場合には、
![$ K[X]/(p(X))$](img12.png)
は
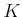
と同型とは限らないことを示しなさい。
問題 8.5
有理数体
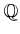
の部分集合
![$ {\mbox{${\mathbb{Z}}$}}[1/5]=\{m/5^n; m\in {\mbox{${\mathbb{Z}}$}}; n=0,1,2,\dots,)$](img16.png)
は
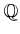
の部分環になることを示しなさい。
問題 8.8
環
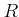
のイデアル
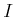
と変数
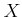
について、次の同型を示しなさい。
問題 8.9
環
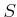
の部分環
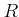
と
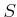
のイデアル
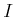
について、
は、
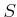
の部分環となることを示しなさい。
問題 8.10
環
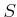
の部分環
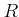
と
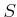
のイデアル
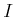
について、
が成り立てば、
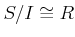
となることを示しなさい。
問題 8.11
環準同型
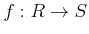
について、
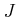
が
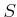
のイデアルであれば、
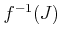
は
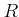
のイデアルとなることを示しなさい。
問題 8.13
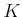
を体とします。このとき同型
![$ K[X,Y]/XK[X,Y]\cong K[Y]$](img34.png)
を示しなさい。
問題 8.14
環
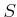
とその部分環
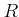
とについて、
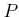
が
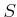
の素イデアルならば、
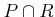
は
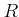
の素イデアルであることを示しなさい。「素イデアル」を「極大イデアル」にかえるとどうか?
問題 8.15
環
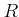
のイデアルに
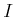
について、
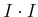
を
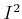
と略記します。
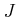
も
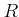
のイデアルで、
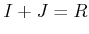
となれば、
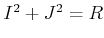
となることを示しなさい。
以下は初等整数論からの補遺です。
問題 8.17
正の整数
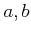
の最大公約数が
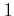
であるための必要十分条件は、
を満たす 整数
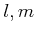
が存在することである。これを示しなさい。
問題 8.18 (この問題に限っては前問が解けている、いないに拘わらず
その結果を使ってよい。(いずれにせよ講義でやるから。)
)
前問を用いて、
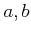
が互いに素ならば、
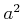
と
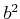
も互いに素であることを示しなさい。
問題 8.19
前問を用いて、
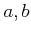
が互いに素ならば、
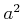
と
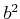
も互いに素であることを示しなさい。
問題 8.20
前問をもちいて、
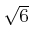
は無理数であることを証明しなさい。ただし、
素因数分解の一意性の知識を用いないで証明すること。
問題 8.21
前問と同じ前提条件で、
一般に、平方数でない(つまり、
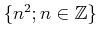
の元ではない)整数
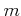
に
たいして、
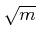
は無理数であることを証明しなさい。
問題 8.22
整数係数の多項式
について、
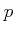
の、 0
でない有理根
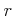
があったとする。
すなわち、
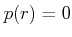
とする。
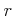
を既約分数
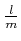
と書いたとき、
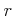 の分子
の分子 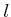 は
は 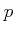 の定数項
の定数項 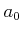 の約数であることを示しなさい。
の約数であることを示しなさい。
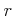 の分母
の分母 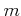 は
は 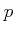 の最高次の係数
の最高次の係数 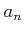 の約数であることを示しなさい。
の約数であることを示しなさい。



Next: About this document ...
2014-12-19
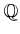
![$ [X]/(X-6) \cong$](img2.png)
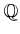 .
.
![$ {\mbox{${\mathbb{Z}}$}}[X]/(X+7) \cong {\mbox{${\mathbb{Z}}$}}$](img3.png) .
.
![$ {\mathbb{C}}[X]/(X-\pi) \cong {\mathbb{C}}$](img4.png) (ただし
(ただし 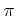 は円周率。)
は円周率。)
![$ {\mathbb{F}}_{11}[X]/(X-4)\cong {\mathbb{F}}_{11}$](img6.png) .
.