Next: About this document ...
微分積分学概論AI要約 No.3
第3回目の主題 :

収束の定義は前回の定義 3.1 で述べた通りである。
それでは定義 3.1 の判定法を満たす 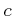 は唯一つだろうか?
は唯一つだろうか?
定理 3.1
数列
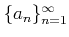
が
(ある人が確かめたところ)
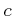
に収束し、
(別の人が確かめたところ) 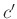
にも収束するなら、
である。つまり、数列の収束先は存在するとしたら唯一つしかない。
そこで、つぎのように定義することができる。
定義 3.2
数列
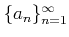
がある数
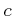
に収束するとき、
と書いて、
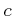
のことを
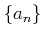
の
極限と呼ぶ。
定理 3.4
収束する数列は有界である。
定理 3.5
実数列
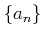
,
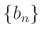
はそれぞれ収束するとする。このとき、
- 「極限をとる」という操作は線形である。すなわち、
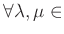
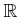 に対して
に対して
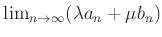 は収束して、
は収束して、
- 「実数の乗法は連続である。」
- 実数の除法は「連続」である。 もっと詳しく言うと、
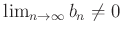 なら、
有限個の例外を除いて
なら、
有限個の例外を除いて 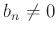 であって、
であって、
上の定理は、どちらかというと特別な二変数関数の連続性に関する
定理として扱うほうが見通しが良い。
二変数関数の連続性については二年生時に詳細に学ぶことになるが、
それまで待っているわけにもいかないので上のようなカッコ「」を用いた
煮え切らない表現
ではあってもここに述べる必要があったというワケ。
問題 3.1
実数列
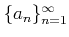
が
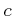
に収束するとき、
は収束すると言えるだろうか。言えるならばその収束先と理由を、言えないならば
反例を作りなさい。
(注意: 今回の講義で証明する定理をただ用いるのではなく、
収束の定義に戻って (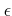 -
-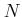 論法で)説明すること。)
論法で)説明すること。)
(ヒント: 2項定理)
付録: 「数列が収束する」ことの証明のフォーマット。
四角の中に埋めるものが肝要。その他、行間に理由付けのための
文章を書く必要がある場合もある。
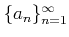 は
は 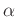 に収束する。
に収束する。
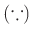
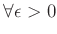 に対して
に対して
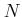 として
として
 を採用する。
すると、この
を採用する。
すると、この 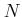 より大きい任意の
より大きい任意の 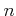 に対して、
に対して、
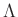
例題 3.6
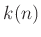
を、
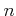
を十進数で表記したときの桁数とする。
とおくと、
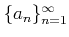
は 0
に収束する。
ARRAY(0xad32748)



Next: About this document ...
2015-04-24
![]()
![]() は唯一つだろうか?
は唯一つだろうか?
![]()
![]() に対して
に対して
![]() として
として
![]() を採用する。
すると、この
を採用する。
すると、この ![]() より大きい任意の
より大きい任意の ![]() に対して、
に対して、