第5回目の主題 :
![]()
次の公理は実数の基本的な性質であった。
数列 ![]() を単なる集合と見てそれが有界かどうか、や
その上限
を単なる集合と見てそれが有界かどうか、や
その上限 ![]() を議論することができる。公理 5.1により、
上に有界な数列は
上限を持つことがわかる。
を議論することができる。公理 5.1により、
上に有界な数列は
上限を持つことがわかる。
がなりたつときにいう。
が成り立つということである。
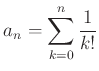
で定義する。このとき
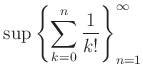
のことを自然対数の底とよび、
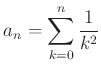
で定義される数列
ヒント: ![]() に対して、
に対して、
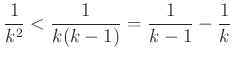
に注意。
|
|
alpha | アルファ | ||
|
|
beta | ベータ | ||
|
|
gamma | ガンマ | ||
|
|
|
delta | デルタ | |
|
|
|
epsilon | イプシロン | |
|
|
|
zeta | ゼータ | |
|
|
|
eta | エータ | |
|
|
|
theta | シータ | |
|
|
|
iota | イオタ | |
|
|
|
kappa | カッパ | |
|
|
|
lambda | ラムダ | |
|
|
|
mu | ミュー | |
|
|
|
nu | ニュー | |
|
|
|
xi | グザイ | |
|
|
|
omicron | オミクロン | |
|
|
|
pi | パイ | |
|
|
|
rho | ロー | |
|
|
|
sigma | シグマ | |
|
|
|
tau | タウ | |
|
|
|
upsilon | ウプシロン | |
|
|
|
phi | ファイ | |
|
|
|
chi | カイ | |
|
|
|
psi | プサイ | |
|
|
|
omega | オメガ |