![]() 《生成される(部分)群》
《生成される(部分)群》
群 ![]() と、その部分集合
と、その部分集合 ![]() とが与えられているとする。このとき、
とが与えられているとする。このとき、
![]()
![]() で生成される
で生成される ![]() の部分群とは、
の部分群とは、
![]() を含む最小の部分群のことである。
を含む最小の部分群のことである。
![]() 特に、
特に、![]() 自身が
自身が ![]() で生成される
で生成される ![]() の部分群であるとき、
単に、
の部分群であるとき、
単に、![]() は
は ![]() で生成される。という。
で生成される。という。
《生成される部分群》の正確な定義は次のようになる。
群 ![]() とその部分集合
とその部分集合 ![]() とが与えられているとする。
とが与えられているとする。
![]() の部分群
の部分群 ![]() が
が ![]() で生成される
で生成される ![]() の部分群であるとは、
次の条件を満たすときに言う。
の部分群であるとは、
次の条件を満たすときに言う。
![]()
![]() が、
が、![]() を部分集合として含む
を部分集合として含む ![]() の部分集合であれば、
の部分集合であれば、
![]() は
は ![]() の部分群になる。
の部分群になる。
![]()
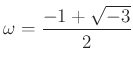 .
.
に一致する。これはもう少し詳しく見ると次の2つの場合がある。
(1)の場合には、 ![]() の位数は無限であるという。
の位数は無限であるという。