


Next: About this document ...
1=6
代数学 IA No.6要約
 《有限群の部分群(オイラー・ラグランジュの定理)》
《有限群の部分群(オイラー・ラグランジュの定理)》
命題 6.1
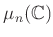
の部分群
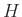
の元の個数は必ず
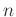
の約数である。
状況を観察するために、次の例を考えよう。
一般の群についても同じようなことが言える:
定理 6.3 (オイラー・ラグランジュ)
有限群
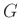
の部分群
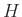
が与えられたとする。このとき、
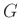 は
は 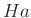 の形の部分集合の互いに交わらない和集合である。
の形の部分集合の互いに交わらない和集合である。
- 各「クラス」
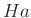 の元の数は
の元の数は 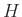 の元の数と等しい。
の元の数と等しい。
- 異なる「クラス」
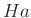 の数(上の
の数(上の 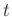 のこと)を
のこと)を ![$ [G:H]$](img16.png) と書くことにすると、
と書くことにすると、
が成り立つ。
2015-05-25
![]() 《有限群の部分群(オイラー・ラグランジュの定理)》
《有限群の部分群(オイラー・ラグランジュの定理)》