


Next: About this document ...
1=7
代数学 IA No.7要約
 《置換群》
《置換群》
置換
は、 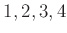 がそれぞれ《変身》して
がそれぞれ《変身》して 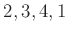 になると
言う操作であって、これを、
になると
言う操作であって、これを、
というようにも書く。
二つの置換の結合(演算)は通常《後ろから読》む。たとえば、
の掛け算 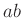 は、
は、
つまり、例えば 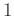 は
は 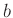 で
で 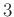 に化けて、次に
に化けて、次に 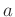 で
で 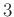 は
は 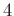 に化けるので、
結果として
に化けるので、
結果として 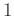 は
は 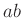 によって
によって 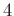 に化けることになる。
に化けることになる。
いくつかの元
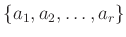 を順繰りに変える置換、すなわち
を順繰りに変える置換、すなわち
のことを
巡回置換と呼び、
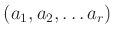 と書き表す。
と書き表す。
定義 7.1
集合
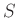
が与えられたとする。このとき
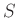
から
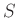
への全単射の全体は
写像の合成に関して群をなす。これを
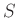
上の
対称群と言う。
有限集合上の対称群を有限対称群と呼ぶ。
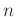
個の元からなる
集合
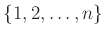
の上の対称群を、
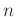 次の対称群
次の対称群と呼び、
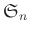
で書き表す。
要は、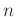 個の元
個の元 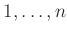 の置換全体のなす群が
の置換全体のなす群が 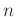 次の対称群である。
次の対称群である。
定理 7.2
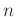
次の対称群の位数は
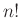
である。
定義 7.3
対称群
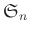
の部分群のことを
置換群という。
任意の置換は互いに同じ文字を含まない巡回置換の積として表すことができる。例えば
、置換
をよくみてみると、次のような変身の様子が分かる。
したがって、
であることが分かる。
置換の概念および記号は、
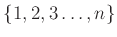 のような集合だけではなく、
他の集合でも使える。
のような集合だけではなく、
他の集合でも使える。
たとえば、
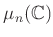 の元を一斉に
の元を一斉に
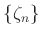 倍することは
倍することは
なる置換に対応する。
2015-06-02
![]() 《置換群》
《置換群》
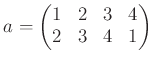
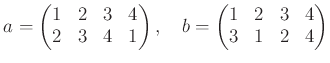
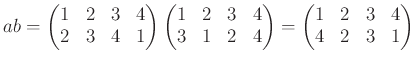
![]() を順繰りに変える置換、すなわち
を順繰りに変える置換、すなわち
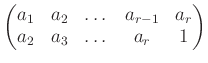
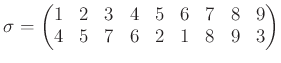
![]() のような集合だけではなく、
他の集合でも使える。
のような集合だけではなく、
他の集合でも使える。
![]() の元を一斉に
の元を一斉に
![]() 倍することは
倍することは