◎ 今回は ruby で行列を用いる。 require "matrix" と書くことで行列が使えるようになる。
◎ ユークリッドの互除法(初級)
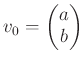
に対して、
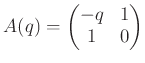
とおくと、
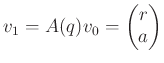
○ ruby による ![]() の実装例(ruby では大文字小文字を
区別する。ここでは小文字の変数や関数しか扱わないことにする 。)
の実装例(ruby では大文字小文字を
区別する。ここでは小文字の変数や関数しか扱わないことにする 。)
def amatrix(q) return(Matrix[[-q,1],[1,0]]) end
◎ 拡張されたユークリッドの互除法
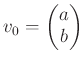
から出発して、
の形のベクトルを得るのが前の問題の趣旨であった。
今度は ![]() の他にもうひとつ単位行列
の他にもうひとつ単位行列 ![]() をならべる。
をならべる。
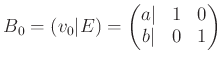
これを何度か繰り返せば、
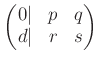
という行列を得る。これをうまく利用せよ。
## $B%W%m%0%i%`Nc(B
require "matrix"
def amatrix(q)
return(Matrix[[-q,1],[1,0]])
end
def gojoho(a,b)
v=Vector[a,b]
m=Matrix.I(2) ###m$B$N=i4|CM$OC10L9TNs(B
while (true) ###$BL58B%k!<%W(B
if (v[0]==0) then ### == $B$KCm0U!#(B
return([v[1],m]) ### v[0]=0 $B$J$iC&=P(B
end
q1=v[1].div(v[0])
m1=amatrix(q1)
v=m1*v
m=m1*m
end
end
### $B<B9TNc(B
p gojoho(113,25)
最終問題:
![]() と
と ![]() とおくとき、
とおくとき、![]() の最大公約数
の最大公約数 ![]() と、
と、
![]() を満たす整数の組
を満たす整数の組 ![]() の例をあげよ。
の例をあげよ。