


Next: About this document ...
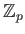 ,
,
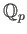 , and the ring of Witt vectors
, and the ring of Witt vectors
Yoshifumi Tsuchimoto
No.03:
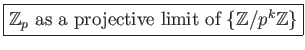
DEFINITION 03.1
An ordered set
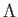
is said to be
directed if
for all
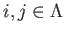
there exists
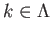
such that
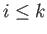
and
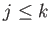
.
DEFINITION 03.2
Let
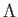
be a directed set.
Let
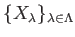
be a family of topological rings.
Assume we are given for each pair of elements
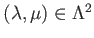
such that
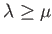
,
a continuous homomorphisms
We say that such a system
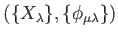
is
a
projective system of topological rings
if it satisfies the following axioms.
-
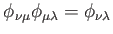 (
(
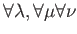 such that
such that
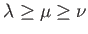 ).
).
-
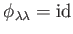 (
(
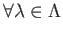 ).
).
DEFINITION 03.3
Let
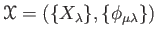
be a projective system of
topological rings. Then we say that a
projective limit
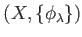
of
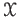
is given if
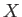 is a topological ring.
is a topological ring.
-
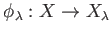 is a continuous homomorphism.
is a continuous homomorphism.
-
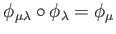 for
for
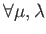 such that
such that
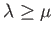 .)
.)
-
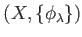 is a universal object among objects which satisfy (1)-(3).
is a universal object among objects which satisfy (1)-(3).
The ``universal'' here means the following:
If
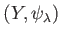 satisfies
satisfies
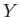 is a topological ring.
is a topological ring.
-
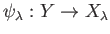 is a continuous homomorphism.
is a continuous homomorphism.
-
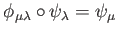 for
for
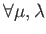 such that
such that
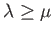 .)
.)
Then there exists a unique continuous homomorphism
such that
PROPOSITION 03.4
For any projective system of topological rings, a projective limit
of the system exists. It is unique up to a unique isomorphism.
(Hence we may call it the projective limit of the system.)
DEFINITION 03.5
For any projective system
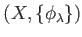
of topological rings,
We denote the projective limit of it by
Note: projective limits of systems of topological spaces, rings, groups,
modules, and so on, are defined in a similar manner.
THEOREM 03.6
as a topological ring.
COROLLARY 03.7
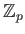 is a compact space.
is a compact space.
Note:
There are several ways to prove the result of the above corollary.
For example,
the ring
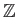 with the metric
with the metric 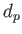 is easily shown to be totally bounded.
is easily shown to be totally bounded.
PROPOSITION 03.8
Each element of
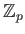 is expressed uniquely as
is expressed uniquely as
EXERCISE 03.1
Is
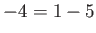
invertible in
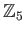
?
(Hint: use formal expansion
is it possible to write down a correct proof to see that the result is true?)



Next: About this document ...
Yoshifumi Tsuchimoto
2016-05-10
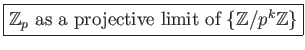
![]() satisfies
satisfies
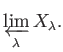
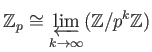
![]() with the metric
with the metric ![]() is easily shown to be totally bounded.
is easily shown to be totally bounded.