Before proceeding further, let me illustrate the idea.
Proposition 9.5 tells us an existence of
a set
![]() of
idempotents in
of
idempotents in
![]() such that its order structure is
somewhat like the one found on the set
such that its order structure is
somewhat like the one found on the set
![]() .
Knowing that the idempotents correspond to decompositons of
.
Knowing that the idempotents correspond to decompositons of
![]() ,
we may ask:
,
we may ask:
To answer this problem, it would probably be better to find out what the set
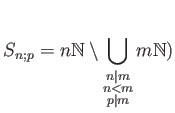
should be. The answer is given by a fact which we know very well: every positive integer may uniquely be written as
Knowing that, we see that the set
The answer to the problem is now given as follows:
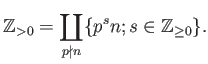
The same story applies to the ring
![]() of universal Witt vectors for
a ring
of universal Witt vectors for
a ring ![]() of characteristic
of characteristic ![]() .
We should have a direct product expansion
.
We should have a direct product expansion
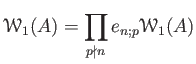
where the idempotent
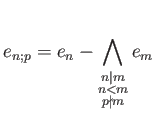
Of course we need to consider infimum of ininite idempotents. We leave it to an excercise:
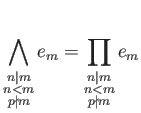
converges.
![$\displaystyle f=
\bigvee
_{\substack{
n>1\\
p \nmid n
}}
e_n
(=[1]-
\prod_
{\substack
{p \nmid n\\
n>1
}}
([1]- e_n))
$](img78.png)
Then ![]() defines a direct product decomposition
defines a direct product decomposition
We call the factor algebra
![]() the
ring
the
ring
![]() of
of ![]() -adic Witt vectors.
-adic Witt vectors.
The following proposition tells us the importance of
the ring of ![]() -adic Witt vectors.
-adic Witt vectors.
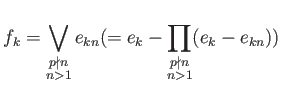
Then ![]() defines a direct product decomposition
defines a direct product decomposition
Furthermore, the factor algebra